Теорема Шеннона для дискретного канала с шумом

Данная теорема является фундаментальным положением Теории Информации и называется так же основной теоремой кодирования Шеннона. Она может быть сформулирована следующим образом: если производительность источника сообщений H¢ (U) меньше пропускной способности канала С т.е. H¢(U)< C, то существует такая система кодирования которая обеспечивает возможность передачи сообщений источника со сколь угодно малой вероятностью ошибки (или со сколь угодно малой ненадежностью).

Если H¢(U) > C, то можно закодировать сообщение таким образом, что ненадежность в единицу времени будет меньше чем H¢(U)-C+ e, где e ®0 (прямая теорема).

Не существует способа кодирования обеспечивающего ненадежность в единицу времени меньшую, чем H¢(U)-C (обратная теорема).

В такой формулировке эта теорема была дана самим Шенноном. В литературе часто вторая часть прямой теоремы и обратная теорема объединяются в виде обратной теоремы сформулированной так: если H¢(U) > C, то такого способа кодирования не существует.

Физический смысл эффекта повышения вероятности при увеличении длительности кодируемых сообщений вытекающего из доказательства прямой теоремы заключается в том, что с ростом Т увеличивается степень усреднения шума действующего в канале и, следовательно, уменьшается степень его мешающего воздействия. Кодирование сообщений длительности Т способом, предполагаемым при доказательстве теоремы Шеннона может начаться лишь тогда, когда сообщение целиком поступило на кодирующее устройство. Декодирование может начаться, когда вся принятая последовательность поступила на декодирующее устройство. Поэтому задержка сообщений во времени между пунктами связи t_зад=2T+t₀, где t₀ - время затрачиваемое на кодирование. Декодирование и прохождение по каналу. При большом Т можно принять, что t_зад=2Т. Из доказательства теоремы (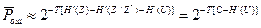, где Z – ансамбль входных сигналов дискретного канала) следует важный результат: верность связи тем выше (меньше вероятность ошибки), чем длиннее блок кодированной последовательности (т.е. тем больше разность С-H¢(U) определяющей запас пропускной способности канала). Итак, следует принципиальная возможность обмена между вероятностью, задержкой и скоростью передачи информации. На практике сложность кодирования и декодирования существенно возрастают с ростом Т поэтому в современных условиях чаще предпочитают иметь умеренное значение Т и добиваться увеличения вероятности за счет менее полного использования пропускной способности канала.

Date: 2016-08-30; view: 366; Нарушение авторских прав