Свойства скалярного произведения.

1. Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов и .

Очевидно, из определения скалярного произведения:

.

1. Для любого числа λ и любых векторов имеем:

.

1. Для любых векторов выполняется равенство .
2. Для любого вектора выполняется соотношение .

Из этого свойства в частности следует .

1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда равен нулю один из сомножителей или векторы перпендикулярны.

Это свойство очевидно из определения скалярного произведения.

Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.

Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора и .

Рассмотрим сначала все возможные скалярные произведения векторов 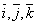друг на друга.

Поэтому

Итак, скалярное произведение векторов равно сумме произведений соответствующих координат: .

Это соотношение позволяет вычислить длину вектора через его координаты:

.

Далее из определения скалярного произведения находим

.

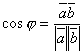Выражая скалярное произведение и длины векторов через их координаты, получим формулу для нахождения косинуса угла между векторами

.

Условие ортогональности двух векторов:

или .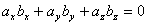

Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.

Примеры.

1. При каком значении m векторы и перпендикулярны?

Условие ортогональности двух векторов .

. Следовательно, m = 15.

Date: 2016-08-30; view: 366; Нарушение авторских прав