
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм методов штрафных функций
|
|
Шаг 1. Задать значения N, J, K, e1, e2, e3, xo, Ro,
где
e1, e2, e3 - соответственно параметры окончания процедур одномерного и многомерного поиска безусловной оптимизации, а также работы алгоритма штрафных функций;
xo - начальное приближение для x*;
Ro - начальный выбор штрафных параметров.
Шаг 2. Построить P(x,R) = W(x) + W(R,g(x),h(x)).
Шаг 3. Найти xt+1 минимизирующее значение P(xt+1,Rt) при фиксированном Rt. В качестве начальной точки использовать xt, а в качестве параметра окончания шага - константу e2 (возможно и e1).
Шаг 4. Проверить, выполняется ли условие |P(xt+1,Rt)-P(xt,Rt-1)|£e3.
· если “да” - положить xt+1=xT и закончить процесс решения;
· если “нет” - перейти к следующему шагу.
Шаг 5. Положить Rt+1=Rt+DRt в соответствии с используемым правилом пересчета, после чего вернуться к шагу 2.
13.4.3. Методы прямого поиска
В методах прямого поиска ограничения учитываются в явном виде. Необходимость разработки этих методов связана с тем, что в инженерных приложениях часто приходится сталкиваться с случаями, когда целевые функции не заданы в явном виде. Эти методы строятся на интуитивных соображениях, не подкреплены строгой теорией и, следовательно, не гарантируется их сходимость. Несмотря на это, в силу своей логической простоты эти методы легко реализуются.
Перед непосредственным применением методов прямого поиска необходимо провести ряд мероприятий по подготовке задачи к решению, а именно:
· исключить ограничения в виде равенств;
· определить начальную допустимую точку.
Простейший способ исключения ограничений в виде равенств заключается в решении его относительно одной из переменных с последующим исключением этой переменной путем подстановки полученного выражения в соотношения, описывающие задачу. При этом следует учитывать, что границы значений исключаемых переменных сохраняются в задаче в виде ограничений - неравенств.
Несмотря на то, что подстановка является самым простым способом исключения ограничений - равенств, не всегда оказывается возможным ее осуществить. В этом случае проблема решается путем численного решения уравнения относительно зависимых переменных при заданных значениях независимых оптимизирующих переменных.
Для определения начальной допустимой точки целесообразно использовать процедуру случайного поиска, основная идея которого будет рассмотрена ниже.
После проведения процедуры подготовки задачи к решению следует приметить один из методов условной оптимизации. Рассмотрим два метода прямого поиска:
· метод комплексов;
· метод случайного поиска.
Метод комплексов
Алгоритм:
Заданы границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи), допустимая точка xo, параметр отображения a (рекомендуется a=1,3) и параметры окончания вычислений e и d.
Шаг 1. Построение начального комплекса, состоящего из P допустимых точек(рекомендуется P=2N). Для каждой точки p = 1, 2,...,P-1:
a) случайным образом определить координаты xp;
b) если xp - недопустимая точка, то найти центр тяжести xцт уже найденных точек и положить xp = xp + 0.5 (xцт - xp); повторять процедуру до тех пор, пока xp не станет допустимой;
c) если xp - допустимая точка, повторять a) до тех пор, пока p=P;
d) вычислить W(xp) для p=0,1,...,P-1.
Шаг 2. Отражение комплекса:
a) выбрать точку xR, для которой W(xR) = max W(xp) = Wmax (решается задача минимизации);
b) найти центр тяжести xцт и новую точку xm = xцт + a (xцт - xR);
c) если xm - допустимая точка и W(xm)³Wmax, то уменьшить в два раза расстояние между xm и центром тяжести xцт, продолжать поиск, пока W(xm)<Wmax;
d) если xm - допустимая точка и W(xm)<Wmax, то перейти к шагу 4;
e) если xm - недопустимая точка, то перейти к шагу 3.
Шаг 3. Корректировка для обеспечения допустимости:
a) если xim < xiL(нижняя граница допускаемой области), то положить xim = xiL; если xim > xiU(верхняя граница допускаемой области), то положить xim = xiU;
b) если xm - недопустимая точка, то уменьшить в два раза расстояние до центра тяжести; продолжать до тех пор, пока xm не станет допустимой точкой.
Шаг 4. Проверка условий окончания вычислений:
a) положить 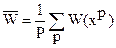 и
и 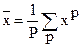 ;
;
b) если 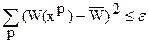 и
и 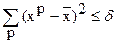 , то вычисления прекратить; в противном случае перейти к шагу 2a.
, то вычисления прекратить; в противном случае перейти к шагу 2a.
Методы случайного поиска
Наиболее простой процедурой случайного поиска является прямая выборочная процедура, заключающаяся в разыгрывании на ЭВМ последовательности точек с координатами
xi = xiL +ri (xiU - xiL), i=1,2,...,N, (13.20)
где
ri - случайная величина, равномерно распределенная на интервале [0,1].
После проверки каждой точки на допустимость вычисляются значения целевой функции, которые сравниваются с наилучшим значением, полученным к данному моменту. Если текущая точка дает лучшее значение, то она запоминается, в противном случае - отбрасывается. Процесс прекращается после заданного числа итераций N или по исчерпанию заданного машинного времени. Для получения 90% доверительного интервала величиной ei (xiU - xiL), где 0<e<1, для переменной xi совместный случайный поиск требует
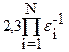
испытаний. При N=5, ei=0,01 число испытаний оценивается в 2,3 1010, что исключает возможность непосредственного использования метода.
Значительного увеличения эффективности процедуры случайного поиска можно достигнуть путем группировки выборок в серии. При этом наилучшая точка в каждой серии используется как начальная точка следующей серии, точки которой уже выбираются из интервала меньшей величины. Данная процедура получила название выборки со сжатием пространства поиска. Рассмотрим более подробно ее алгоритм.
Заданы границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи), начальные допустимая точка xo и интервал поиска Dxo = xiU - xiL, количество серий Q, количество точек в серии P и параметр окончания вычислений e. Для каждой из серий, начиная с q = 1, необходимо выполнить следующие действия:
Шаг 1. Для i = 1,2,...,N вычислить
xip = xiq-1 +ri Dxq-1,
где
ri - случайная величина, равномерно распределенная на интервале [-0,5,0,5].
Шаг 2.
· Если xp - недопустимая точка и p < P, то повторить шаг 1.
· Если xp - допустимая точка, то запомнить xp и W(xp) и
· если p < P, то повторить шаг 1.
· если p = P, то найти среди всех допустимых точек xp точку с наименьшим значением W(xp) и положить ее равной xq.
Шаг 3. Уменьшить интервал поиска, полагая Dxiq = ei Dxiq-1.
Шаг 4.
· Если q > Q, то закончить вычисления.
· В противном случае увеличить q = q + 1 и продолжить вычисления, начиная с шага 1.
13.4.4. Методы линеаризации
Идея методовзаключается в сведении задачи нелинейного программирования к задаче линейного программирования. С этой целью нелинейные функции целевой функции W(x) и ограничений g(x), h(x) в ряд Тейлора до членов первого порядка в окрестности точки линеаризации xt, что позволяет W(x), g(x), h(x) аппроксимировать линейными функциями и свести общую задачу нелинейного программирования
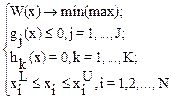
к следующей задаче линейного программирования
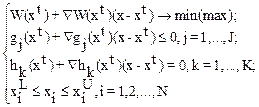
Решая ее при помощи методов линейного программирования, находим новое приближение xt+1. В случае нелинейных функций точка xt+1 -обычно недопустимая точка. Однако для сходимости к оптимуму достаточно, чтобы последовательность точек {xt}, полученных в результате решения последовательности подзадач линейного программирования, выполнялось следующее условие: значение целевой функции W и невязки по ограничениям в xt+1 должно быть меньше их значений в точке xt.
Date: 2016-07-25; view: 604; Нарушение авторских прав