
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример 13.6. Приложение метода хорд к задаче оптимального раскроя бревна на брус.
|
|
W(l)=(l/2)(dk -(dk-do)l/lo)2 ® max,
где
lo=0,10,
dk =0,22,
do =0,12
в интервале 5£l£9 (см. пример 3.3) при e=0,0001.
W’(l) = dW(l)/dl = 0,0242 – 0,0044 l + 0,00015 l2.
Итерация 1.
Шаг 1. W’(5)=0,00595, W’(9) = -0,00325, N=9, P=5.
Шаг 2. R=5-{(0,00595*(5-9))/(0,00595+0,00325)}=7,587.
Шаг 3. W’(7,587)= -0,00055<0; |W’(7,587)| ³ 0,0001, положить N=7,587.
Итерация 2.
Шаг 2. R=5-{(0,00595*(5-7,587))/(0,00595+0,00055)}=7,368.
Шаг 3. W’(7,368)= -0,000076<0; |W’(7,368)| £ 0,0001, решение l*=7,368, при котором W*(7,368)= 0,0789, найдено с заданной точностью.
Метод касательных
Сущность метода. Ориентирован на нахождение корня уравнения W’(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны (рис.13.4). Работа алгоритма начинается из точки xo, которая представляет начальное приближение корня уравнения W’(x)=0. Далее строится линейная аппроксимация функции W’(x) в точке x1, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. Если точка xk принята в качестве текущего приближения к оптимальной точке, то линейная функция, аппроксимирующая функцию W’(x) в точке xk, записывается в виде
W’(x,xk) = W’(xk) + W’’(xk)(x-xk). (13.4)
Приравняв правую часть уравнения к нулю, получим следующее приближение к искомой точке:
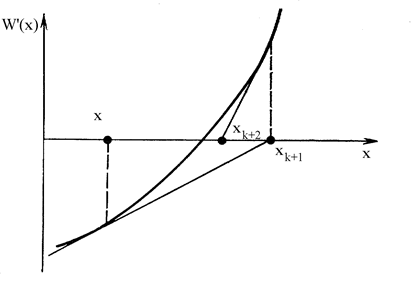
Рис. 13.4. Схема метода касательных
Шаг 1. Следующее приближение к стационарной точке x* определяется по формуле:
xk+1 = xk - [W’(xk)/W’’(xk)].
Шаг 2. Вычислить W’(xk+1), W’’(xk+1)
Шаг 3. Если |W’(xk+1)| < e, то закончить поиск. В противном случае необходимо вернуться к шагу 1.
Как явствует из алгоритма, целевая функция W(x) должна быть
дважды дифференцируема.
Пример 13.7. Приложение метода касательных к задаче оптимального раскроя бревна на брус.
W(l)=(l/2)(dk -(dk-do)l/lo)2 ® max,
где
lo=0,10,
dk =0,22,
do =0,12
в интервале 5£l£9 (см. пример 3.3) при e=0,0001.
W’(l) = dW(l)/dl = 0,0242 – 0,0044 l + 0,00015 l2.
W’’(l) = dW’(l)/dl = – 0,0044 + 0,0003 l.
Итерация 1.
Шаг 1. l1=5; W’(5)=0,00595, W’’(5) = -0,0029, l2=5-(0,00595/-0,0029)=7,052;
Шаг 2. |W’(7,052)|= 0,000631³ 0,0001.
Итерация 2.
Шаг 1. l1=7,052; W’(7,052)= 0,000631, W’’(7,052) = -0,00228,
l3=7,052-(0,000631/-0,00228)=7,329;
Шаг 2. |W’(7,329)|= 0,00000954£ 0,0001, решение l*=7,329, при котором W*(7,329)= 0,0789, найдено с заданной точностью.
Date: 2016-07-25; view: 516; Нарушение авторских прав