Безусловная однопараметрическая оптимизация

Несмотря на то, что безусловная оптимизация функции одной переменной- наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итеративных процедур многопараметрической оптимизации.

Пример 13.1. Оптимальный раскрой лесоматериалов.

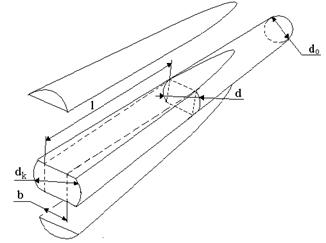
Бревно длиной 15 м имеет форму конуса, диаметры оснований которого равны соответственно 0,4 и 0,2 м. Требуется автоматизировать процесс раскроя бревна для получения бруса квадратного поперечного сечения, ось которого совпадала бы с осью бревна и объем которого был бы наибольшим. Определить размеры бруса (рис. 13.1).

Рис. 13.1. Оптимизация раскроя бревна

Постановка задачи.

1. В качестве показателя эффективности целесообразно взять объем бруса, м³.

2. В качестве управляемой переменной задачи следует взять длину бруса l. При этом длина бруса l связана с поперечным размером b следующими зависимостями:

d = d _k - (d _k- d _o) l / l _o; b ²= d ²/2,

где

d _k - диаметр бревна в комле, м;

d _o - диаметр бревна в вершине, м;

l _o - длина бревна, м.

3. Целевая функция:

W(l)=(l /2)(d _k -(d _k- d _o) l / l_o)² ® max.

Пример 13.2. Планирование борьбы с лесными пожарами

Лесной пожар распространяется фронтом огня шириной H км со скоростью v км/час. Задержать наступление огня можно путем построения противопожарной перегородки, пересекающей лес по всей ширине. Один рабочий может построить l км перегородки в час. Затраты на транспортировку каждого рабочего с необходимым оборудованием к месту пожара и обратно составляют T руб.; оплата труда каждого рабочего составляет s руб. в час. Удельные потери от прохождения огня оцениваются в q руб./га. Сколько рабочих следует послать на борьбу с огнем, чтобы полные издержки были минимальны?

Постановка задачи.

1. В качестве показателя эффективности целесообразно взять полные затраты на построение противопожарной загородки, руб, включающие в себя транспортные расходы W_т и оплату труда рабочих W_о, а также потери лесных угодий от огня W_л.

2. В качестве управляемой переменной задачи следует взять потребное число рабочих для тушения пожара n.

3. Целевая функция:

W(n)= W_т +W_о +W_л = T×n + (H× s)/ l + (100× H ² × v)/(n× l) ® min.

Своеобразным индикатором важности методов оптимизации функции одной переменной является огромное множество реализованных алгоритмов, которые условно можно сгруппировать следующим образом:

· методы исключения интервалов;

· методы полиномиальной аппроксимации;

· методы с использованием производных.

Date: 2016-07-25; view: 641; Нарушение авторских прав