
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Двухфакторный комплекс
|
|
Рассмотрим влияние двух факторов: А, градации (или уровни) которого обозначены Ai (i=1…m) и B с уровнями B j (j=1…k). При этом каждое наблюдение можно обозначить через xij, где i - уровень фактора A, j - номер наблюдения. Исходные данные удобно представить в виде табл. 5.2.
Таблица 5.2
| Bj | Ai | MjB | |||
| A1 | A2 | … | Am | ||
| B1 | x11 | x12 | … | x1m | M1 |
| B2 | x21 | x22 | … | x2m | M2 |
| … | … | … | … | … | … |
| Bk | xk1 | xk2 | … | xkm | Mk |
| MiA | M1 | M2 | … | Mm |
Общая схема дисперсионного анализа двухфакторных комплексов в принципе не отличается от описанных схем однофакторного дисперсионного анализа. Анализ двухфакторных комплексов не меняет, а лишь несколько усложняет расчеты, поскольку наряду с действием каждого фактора в отдельности приходится учитывать и их совместное действие на результативный признак. Однако следует строго выполнять требование независимости факторов. Нельзя подвергать дисперсионному анализу корреляционно связанные признаки, такие, например, как высота дерева и объем его стволовой части.
В двухфакторных дисперсионных комплексах определяются четыре дисперсии.
1) Общая дисперсия равна сумме центральных отклонений вариант xij от общей средней по комплексу M:
s0 2=  (xij – M)2. (5.6)
(xij – M)2. (5.6)
2) Дисперсия по первому фактору (A) равна сумме взвешенных квадратов центральных отклонений частных средних по градациям первого фактора от общей средней по всему комплексу:
sA 2=  (MiA –M)2, (5.7)
(MiA –M)2, (5.7)
где
m - число наблюдений по фактору А одной градации;
MiA - частные средние значения по градациям фактора A;
M - общее среднее значение для всего комплекса.
3) Дисперсия по второму фактору (B) равна сумме взвешенных квадратов центральных отклонений частных средних по градациям второго фактора от общей средней по всему комплексу:
sB 2= 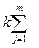 (MjB–M)2, (5.8)
(MjB–M)2, (5.8)
где
k - число наблюдений по фактору B одной градации;
MjB - частные средние значения по градации фактора В;
M - общее среднее значение для всего комплекса.
4) Дисперсия по сочетанию градаций sAB 2 дает меру разнообразия эффектов второго признака (его градаций) при разных градациях первого признака.
Так как в ортогональных (равномерных и пропорциональных) дисперсионных комплексах все дисперсии находятся в определенной связи, то сумма частных дисперсий, рассчитанных независимо, равна общей дисперсии:
sAB 2 = s0 2 - sA 2 - sB 2, (5.9)
где
s0 2 - общая дисперсия;
sA 2 - дисперсия по первому фактору;
sB 2 - дисперсия по второму фактору.
Отношения (5.10) и (5.11) используют в качестве статистической характеристики критерия.
F = 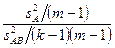 (5.10)
(5.10)
и
F = 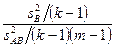 (5.11)
(5.11)
Если вычисленное значение F меньше табличного при уровне значимости a, то гипотезу об отсутствии влияния фактора А или B принимают. Стандартные значения критерия F приведены в приложениях 6 и 7.
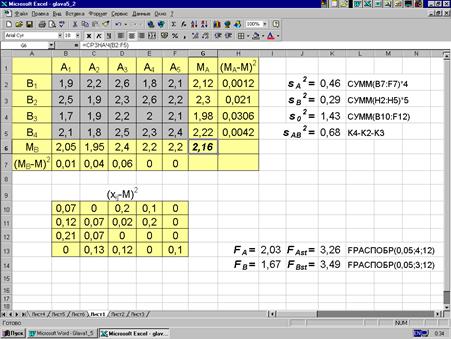
Рис. 5.2.
Пример 5.4. Рассмотрим результаты влияния пяти различных удобрений (фактор А) и четырех типов почв (фактор В) на прирост древостоя, представленные в MS Excel (рис. 5.2). Требуется установить, есть ли основание считать, что прирост на разных типах почвы не зависит от вида удобрения и что эффективность разных удобрений различна независимо от типа почвы. На рис. 5.2 приведены все необходимые расчеты. Поскольку для обоих факторов при уровне значимости a=0,05 и соответствующих степенях свободы Fф < Fst (получены с помощью функции FРАСПОБР), то следует считать, что нулевая гипотеза не отвергается, то есть вариации могли иметь случайное происхождение.
5.4. Использование MS Excel для проведения дисперсионного анализа
Для вызова программы проведения дисперсионного анализа необходимо выбрать команду "Анализ данных" в меню "Сервис". В списке "Инструменты анализа" (рис. 5.3) выбираем одну из строк:
· "Однофакторный дисперсионный анализ";
· "Двухфакторный дисперсионный анализ с повторениями";
· "Двухфакторный дисперсионный анализ без повторений".
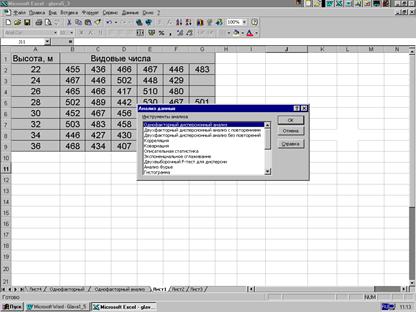 |
Рис. 5.3.
Date: 2016-07-25; view: 761; Нарушение авторских прав