Теории ошибок измерений

Знание функции плотности распределения случайных ошибок измерений дает возможность для решения целого ряда задач, возникающих при различных геодезических работах: определение наиболее вероятного значения при многократных измерениях; установление предельных значений (допусков) для конкретного вида работ; вычисление вероятности появления случайной ошибки в определенном интервале; выявление предельных значений, за которыми ошибки можно квалифицировать как грубые. Для этого воспользуемся функцией Лапласа, имеющей следующий вид

(1.17)

Вероятность того, что любая случайная величина X примет значение, принадлежащее интервалу (a, b), можно выразить через функцию распределения

(1.18)

Перейдем к нормированной случайной величине t. Неравенства a < x < b и равносильны. Поэтому вероятности этих неравенств равны между собой

(1.19)

Используя равенство (1.18), запишем

(1.20)

где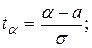

Считая, что нормированная случайная величина t имеет нормальное распределение, и используя определение интегральной функции , получим

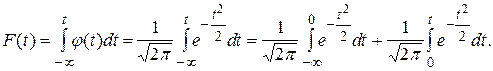(1.21)
Первое слагаемое числено равно половине площади под нормированной кривой распределения; второе слагаемое является выражением функции Лапласа. Итак, для нормально распределенной случайной величины имеем

(1.22)

Используя формулу (1.22) в выражении (1.20), получим

(1.23)

1.7. Определение вероятности отклонения случайной
величины от ее математического ожидания

Определим вероятность того, что нормально распределенная величина X отклоняется от своего математического ожидания на величину меньшую чем e, т.е. найдем вероятность осуществления неравенства

Перейдя к нормированной случайной величине t, имеем

(1.24)

Согласно равенству (1.23)

(1.25)

Окончательно получим

(1.26)

При равенство (1.26) примет вид

(1.27)

Выразив отклонение случайной величины X в долях среднего квадратического отклонения, т.е. положив равенство (1.26) можно записать

(1.28)

Таким образом, значение 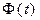при заданном t определяет вероятность того, что отклонение нормально распределенной величины по абсолютному значению меньше

При t = 1 имеем

при t = 2 имеем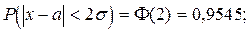

при t = 3 имеем

Из последнего равенства следует, что практически рассеивание случайной величины укладывается на участке Вероятность того, что случайная величина X попадает за этот интервал очень мала, а именно равна 0,0027, т.е. это событие можно считать практически невозможным. На приведенном рассуждении основано “правило трех сигм”, которое формулируется следующим образом: если случайная величина имеет нормальное распределение, то отклонение этой величины от ее математического ожидания по абсолютной величине не превосходит утроенного среднего квадратического отклонения.

Date: 2016-07-25; view: 317; Нарушение авторских прав