
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определенный интеграл, вычисление площадей
|
|
1. Понятие определенного интеграла.
Определенный интеграл – это число, которое находится по формуле Ньютона-Лейбница:
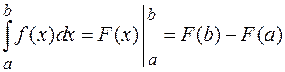 ,
,
где  – первообразная для функции
– первообразная для функции  , то есть
, то есть  ;
;
 ,
,  – нижний и верхний пределы интегрирования, показывающие, как меняется переменная интегрирования х.
– нижний и верхний пределы интегрирования, показывающие, как меняется переменная интегрирования х.
Формула Ньютона-Лейбница связывает определенный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл, т.е. найти первообразную, причем удобно взять произвольную постоянную равной нулю:  , а затем вычислить разность значений этой первообразной в верхнем и нижнем пределах.
, а затем вычислить разность значений этой первообразной в верхнем и нижнем пределах.
Например:
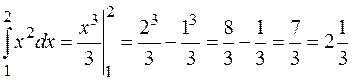 .
.
2. Геометрический смысл определенного интеграла.
Если функция 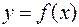 неотрицательная на отрезке
неотрицательная на отрезке 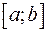 , то
, то
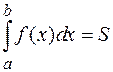 ,
,
где S – площадь под кривой 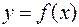 на отрезке
на отрезке 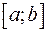 (рис. 8).
(рис. 8).

y y 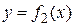
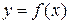
S
S
0 a b x
0 a b x 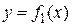
Рис. 8 Рис. 9
3. Вычисление площадей плоских фигур.
Площадь фигуры, заключенной между кривыми 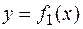 и
и 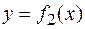 на отрезке
на отрезке 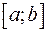 , вычисляется по формуле
, вычисляется по формуле
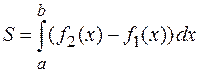 ,
,
при этом 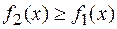 для
для 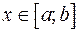 (рис. 9).
(рис. 9).
Задача. Вычислить площадь фигуры, ограниченной линиями
 и
и 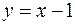 . Сделать чертеж.
. Сделать чертеж.
Решение. Выполним чертеж.
Первое уравнение определяет параболу, а второе – прямую линию.
Для построения параболы найдем координаты ее вершины и точки пересечения ее с осями координат.
Если уравнение параболы  , то вершина параболы находится в точке
, то вершина параболы находится в точке  . В данной задаче
. В данной задаче  ,
,  . Итак, вершина параболы – точка (3;– 4).
. Итак, вершина параболы – точка (3;– 4).
Точки пересечения параболы с осями.
С осью Ox: 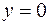 , тогда
, тогда  . Решив квадратное уравнение (прил.1, п. 2), получаем
. Решив квадратное уравнение (прил.1, п. 2), получаем  . Точки пересечения параболы с осью
. Точки пересечения параболы с осью  есть точки (1;0) и (5;0).
есть точки (1;0) и (5;0).
С осью Oy: 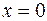 , тогда
, тогда  . Точка пересечения параболы с осью
. Точка пересечения параболы с осью 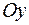 есть точка (0;5).
есть точка (0;5).
Строим параболу по найденным точкам, замечая, что ветви параболы направлены вверх, т.к. 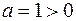 (рис. 10).
(рис. 10).
Прямую 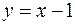 строим по двум точкам, например,
строим по двум точкам, например,
при 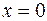
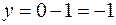 ; при
; при 
 .
.
Получены точки: 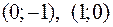 .
.


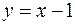
0 1 3 5 6 
–1
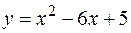
–4
Рис. 10
Найдем точки пересечения параболы и прямой, решив систему уравнений:
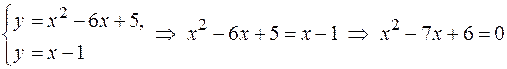 .
.
Решим полученное квадратное уравнение:
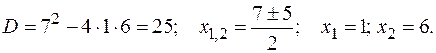
Найдем соответствующие ординаты 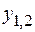 из уравнения y = x –1:
из уравнения y = x –1: 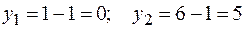 . Итак, точки пересечения параболы и прямой есть точки
. Итак, точки пересечения параболы и прямой есть точки 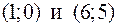 .
.
Заштрихуем плоскую фигуру, ограниченную параболой и прямой (рис.10). Здесь функции 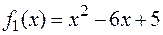 и
и 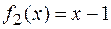 ограничивают фигуру соответственно снизу и сверху, то есть
ограничивают фигуру соответственно снизу и сверху, то есть 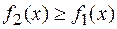 при
при 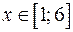 .
.
Для нахождения искомой площади воспользуемся формулой
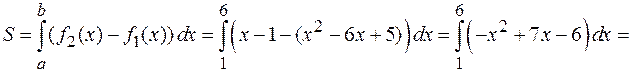
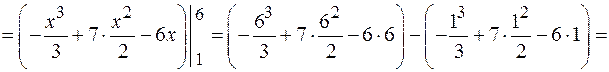
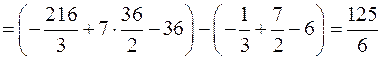 .
.
Ответ. Искомая площадь равна: 
Замечание. Если одна из линий – гипербола, например, xy = –6, то ее можно построить по точкам. Удобно взять точки с абсциссами 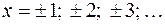 и вычислить соответствующие им ординаты y, в нашем случае по формуле
и вычислить соответствующие им ординаты y, в нашем случае по формуле  .
.
Если в ответе задачи получен логарифм числа, то значение логарифма можно взять из прил.1, п. 9.
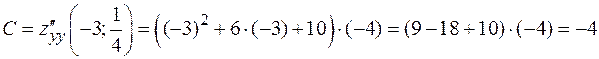 .
.
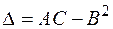
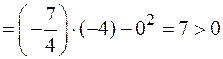 .
.
Следовательно, экстремум в точке  есть. Так как
есть. Так как  , то в точке
, то в точке  – максимум функции.
– максимум функции.
6. Найдем значение функции  в точке максимума:
в точке максимума:
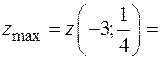
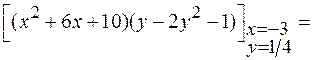
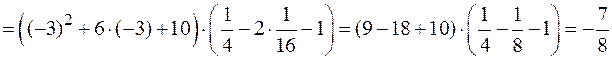 .
.
Ответ. 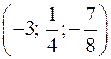 – точка максимума функции
– точка максимума функции  .
.
ЛИТЕРАТУРА
1. Высшая математика для экономистов/ Под ред. Н. Ш. Кремера. – М.: Банки и биржи, 1997.
2. Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. – М.: Наука, 1996.
3. Красс М. С., Чупрынов Б. П. Основы математики и ее приложение в экономическом образовании. – М.: Дело, 2001.
4. Математический анализ: Учебно-методическое пособие. – Новосибирск: СибУПК, 2003.
5. Методические указания по изучению элементарной математики для студентов 1 курса. – Новосибирск: СибУПК, 1989.
6. Письменный Д. Конспект лекций по высшей математике: В 2-х ч. – М.: Рольф, 2000.
ПРИЛОЖЕНИЯ
Приложение 1
Date: 2016-07-25; view: 638; Нарушение авторских прав