Исследование функции

1. Проиллюстрируем на примере некоторые важные свойства графика функции (рис. 4).

Рис. 4

Интервалы монотонности:

· функция возрастает при ;

· функция убывает пр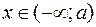и и .

Точки экстремума:

С – точка максимума (max); A – точка минимума (min).

Интервалы выпуклости:

· функция выпуклая при ;

· функция вогнутая при и при .

Точки В и D являются точками перегиба, так как в них происходит смена выпуклости на вогнутость или наоборот.

2. Правило исследования функции y = f(x) на монотонность и

точки экстремума.

а) Вычислить первую производную .

б) Найти критические точки, т.е. точки, в которых производная равна нулю или не существует.

в) Определить знак производной на интервалах между критическими

точками в области определения функции.

г) Сделать выводы о промежутках монотонности функции согласно

признакам монотонности:

если на (a;b), то функция убывает при ,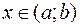

если на (a;b), то функция возрастает при .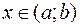

д) Сделать выводы о наличии точек экстремума согласно признаку существования экстремума:

если при переходе слева направо через критическую точку произ­вод­ная меняет знак с плюса на минус, то – точка максимума; если с минуса на плюс, то – точка минимума.

3. Правило исследования функции y = f(x) на выпуклость,

вогнутость и точки перегиба.

а) Вычислить вторую производную .

б) Найти точки, в которых вторая производная равна нулю или не существует, эти точки называются подозрительными на перегиб.

в) Определить знак второй производной на интервалах между найденными точками в области определения функции.

г) Сделать выводы о промежутках выпуклости и вогнутости согласно признакам выпуклости и вогнутости:

если на (a;b), то график функции вогнутый при ,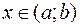

если на (a;b), то график функции выпуклый при .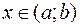

д) Сделать выводы о наличии точек перегиба согласно достаточному условию существования точек перегиба:

eсли при переходе через подозрительную на перегиб точку вторая производная меняет знак, то в этой точке имеется перегиб графика функции.

4. Четность и периодичность функции.

Функция y = f(x) называется четной, если для любых x из области определения функции справедливо равенство f(–x)= f(x), в этом случае график симметричен относительно оси Oy.

Для нечетной функции для любых x из области определения справедливо равенство f(–x)= – f(x), ее график симметричен относительно начала координат.

Функция y = f(x) называется периодической, если существует число такое, что для любых x из области определения функции справедливо f(x+T)= f(x).

Date: 2016-07-25; view: 406; Нарушение авторских прав