
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Двойное лучепреломление
|
|
Все кристаллы, кроме кристаллов кубической система — изотропных кристаллов, являются анизотропными, то есть свойства кристаллов зависят от направления. Явление двойного лучепреломления впервые было обнаружено Барталином в 1667 г. на кристалле исландского шпата (разновидность СаСО3). Явление двойного лучепреломления заключается в следующем: луч света, падающий на анизотропный кристалл, разделяется в нем на два луча: обыкновенный и необыкновенный, распространяющиеся с разными скоростями  в различных направлениях.
в различных направлениях.
Анизотропные кристаллы подразделяются на одноосные и двуосные.
 У одноосных кристаллов имеются одно направление, называемое оптической осью, при распространении вдоль которого не происходит разделения на обыкновенный и необыкновенный лучи. Любая прямая параллельная направлению оптической оси будет также являться оптической осью. Любая плоскость, проходящая через оптическую ось и падающий луч, называется главным сечением или главной плоскостью кристаллам.
У одноосных кристаллов имеются одно направление, называемое оптической осью, при распространении вдоль которого не происходит разделения на обыкновенный и необыкновенный лучи. Любая прямая параллельная направлению оптической оси будет также являться оптической осью. Любая плоскость, проходящая через оптическую ось и падающий луч, называется главным сечением или главной плоскостью кристаллам.
Отличия между обыкновенными и необыкновенными лучами:
1. обыкновенный луч подчиняется законам преломления  необыкновенный - нет;
необыкновенный - нет;
2. обыкновенный луч поляризован перпендикулярно главной плоскости, плоскость поляризации необыкновенного луча перпендикулярна плоскости поляризованного обыкновенного луча;
3. кроме оптической оси обыкновенные и необыкновенные лучи распространяются в разных направлениях. Показатель преломления n 0 обыкновенного луча постоянен во всех направлениях, следовательно, фазовая скорость обыкновенного луча постоянна во всех направлениях. Показатель преломления n е необыкновенного луча (U ф.е.) зависит от направления.
Различие скоростей U о и U е для всех направлений, кроме направления оптической оси, обуславливает явление двойного лучепреломления в одноосных кристаллах. У двуосных кристаллов имеется два направления, вдоль которых не происходит двойного лучепреломления.
Понятие обыкновенного и необыкновенного лучей имеет место пока эти лучи распространяются в кристалле, при выходе из кристалла эти понятия теряют смысл, то есть лучи отличаются только плоскостями поляризаций.

Природа двулучепреломления связана с тем, что обыкновенные и необыкновенные лучи имеют разные скорости, а так как  , то для обыкновенного и необыкновенного лучей будут разные показатели преломления n 0 и n е, а так как
, то для обыкновенного и необыкновенного лучей будут разные показатели преломления n 0 и n е, а так как  то можно сказать, что первопричиной двойного лучепреломления является анизотропия диэлектрической проницаемости кристалла. Кристаллы, у которых V е < V 0 (n е > n 0) называются положительными, а у которых V е > V 0 (n е < n 0)называются отрицательными.
то можно сказать, что первопричиной двойного лучепреломления является анизотропия диэлектрической проницаемости кристалла. Кристаллы, у которых V е < V 0 (n е > n 0) называются положительными, а у которых V е > V 0 (n е < n 0)называются отрицательными.
Поляризованный свет - свет в котором колебания светового вектора, каким то образом упорядочены.
Естественный свет - свет в котором все направления колебания светового вектора Е равновероятны.
Закон Малюса: I=I0*cos2α
Закон Брюстера: Закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера.
Закон Брюстера:  , где n21 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера).
, где n21 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера).
Распространение электромагнитных волн в одноосных кристаллах:
Оптическая ось кристалла - направление в оптически анизотропном кристалле по которому распространяется луч света не испытывая двойного лучепреломления.
Одноосные и двухосные кристаллы - кристаллы с одним или двумя направлениями вдоль которых существует двойное лучепрломление.
Двойное лучепреломление — эффект расщепления в анизотропных средах луча света на две составляющие. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным, второй же отклоняется в сторону, нарушая обычный закон преломления света, и называется необыкновенным.
Поляризационные призмы, один из классов призм оптических. Поляризационные призмы служат линейными поляризаторами — с их помощью получают линейно поляризованное оптическое излучение. Обычно поляризационные призмы состоят из 2 или более трёхгранных призм, по меньшей мере одна из которых вырезается из оптически анизотропного кристалла.
Поляроид, поляризационный светофильтр, один из основных типов оптических линейных поляризаторов; представляет собой тонкую поляризационную плёнку, заклеенную для защиты от механических повреждений и действия влаги между двумя прозрачными пластинками (плёнками).
69. Волновые свойства частиц.
Свет обладает как волновыми, так и корпускулярными свойствами. Волновые свойства проявляются при распространении света (интерференция, дифракция). Корпускулярные свойства проявляются при взаимодействии света с веществом (фотоэффект, излучение и поглощение света атомами).
Свойства фотона как частицы (энергия Е и импульс p) связаны с его волновыми свойствами (частотой ν и длиной волны λ) соотношениями
| E = h ν; p = h ν / c = h / λ, |
где h = 6,63·10–34 Дж·с – постоянная Планка.
Французский физик де Бройль в 1924 г. высказал предположение, что сочетание волновых и корпускулярных свойств присуще не только свету, но и любому материальному телу. Согласно де Бройлю, каждому телу массой m, движущемуся со скоростью υ, соответствует волновой процесс с длиной волны
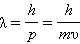
|
(нерялятивистское приближение υ << c).
Наиболее отчетливо волновые свойства проявляются у элементарных частиц. Это происходит потому, что из-за малой массы частиц длина волны оказывается сравнимой с расстоянием между атомами в кристаллических решетках. В этом случае при взаимодействии пучка частиц с кристаллической решеткой возникает дифракция.
Для иллюстрации волновых свойств частиц часто используют мысленный эксперимент – прохождение пучка электронов (или других частиц) через щель ширинойΔ x. С точки зрения волновой теории при дифракции на щели пучок будет уширяться с угловой расходимостью θ ≥ λ / Δ x. С корпускулярной точки зрения уширение пучка после прохождения щели объясняется появлением у частиц некоторого поперечного импульса. Разброс значений этого поперечного импульса («неопределенность») есть
| Δ p x ≈ p θ ≥ (λ / Δ x) p = h / Δ x. |
Соотношение
| Δ p x · Δ x ≥ h |
носит название соотношения неопределенностей. Это соотношение на корпускулярном языке выражает наличие волновых свойств у частиц.
Эксперимент по прохождению пучка электронов через две близко расположенные щели может служить еще более яркой иллюстрацией волновых свойств частиц. Этот эксперимент является аналогом оптического интерференционного опыта Юнга.
Компьютерная модель воссоздает на экране дисплея мысленные эксперименты по дифракции электронов на одной и двух щелях.
Подлетая к экрану со щелями, частицы взаимодействуют с ним как волны де Бройля. Поведение частиц в пространстве между экраном со щелями и фотопластинкой описывается в квантовой физике с помощью Ψ-функций. Квадрат модуля пси-функции определяет вероятность обнаружения частицы в том или ином месте. Таким образом, попадание частиц в различные точки фотопластинки есть вероятностный процесс. Компьютерная модель позволяет продемонстрировать этот процесс.
В случае одиночной щели модель иллюстрирует соотношение неопределенностей, которое является следствием двойственной природы частиц. Можно изменять в некоторых пределах ширину щели и наблюдать дифракционное размытие электронного пучка на фотопластинке.
Предполагается, что электроны имеют энергию порядка 100 эВ.
Обратите внимание, что в случае двух щелей наблюдаемое на фотопластинке распределение не является простым наложением двух независимых распределений от каждой из щелей в отдельности. Появление интерференционных полос на фотопластинке однозначно свидетельствует о том, что каждая достигшая фотопластинки частица одновременно прошла через обе щели экрана.
Гипотеза Луи де Бройля.
В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальный характер. Частицы вещества также обладают волновыми свойствами.
71. Уравнение Шредингера.
| Толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающей движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции, т.к. именно величина осуществляет вероятность пребывания частицы в момент времени t в объеме d V, т.е. в области с координатами x и, y и, z и. Т.к. искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Шредингером.
ШредингерЭрвин(1887–1961) – австрийский физик-теоретик, один из создателей квантовой механики. Основные работы в области статистической физики, квантовой теории, квантовой механики, общей теории относительности, биофизики. Разработал теорию движения микрочастиц – волновую механику, построил квантовую теорию возмущений – приближенный метод в квантовой механике. За создание волновой механики удостоен Нобелевской премии.
Уравнение Шредингера не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы.
Уравнение Шредингера в общем виде записывается так:
где m – масса частицы, i 2 – мнимая единица, – оператор Лапласа – потенциальная энергия частицы в силовом поле, в котором она движется, Ψ – искомая волновая функция. Если силовое поле, в котором движется частица, потенциально, то функция U не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера распадается на два сомножителя, один из которых зависит только от координаты, а другой – только от времени:
Здесь E – полная энергия частицы, которая в случае стационарного поля остается постоянной. Чтобы убедиться в справедливости выражения 4.4.2, подставьте его в выражение, и вы получите уравнение Шредингера для стационарных состояний: , Уравнение Шредингера можно записать в виде. В этом уравнении – оператор Гамильтона, равный сумме операторов. Гамильтониан является оператором энергии E. В квантовой механике другим переменным также и динамическим сопоставляются операторы. Соответственно рассматривают операторы координат, импульса, момента импульса и т.д. |
Физический смысл волновой функции.
Волновая функция зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами.
72. Квантовая энергия.
Квантовая энергетика – энергетика 3-го тысячелетия, использующая энергию квантового излучения в условиях сверхсильного электромагнитного поля. Квантовая энергетика, автономная, мобильная энергетика, как источник получения энергии для использования в промышленном и индивидуальном масштабе, и не зависимо от количества энергии.
Создателем энергетики, как отрасли промышленности 2-го тысячелетия, является Никола Тесла. Энергетика 2-го тысячелетия не обладает мобильностью и минимизной, в основном это доставка энергии от поставщика к потребителю.
Частица в прямоугольной потенциальной яме.
 Рис. 1. Потенциальная яма Рис. 1. Потенциальная яма
|
Потенциальная яма – ограниченная область пространства с пониженной потенциальной энергией частицы. Потенциальная яма обычно отвечает короткодействующим силам притяжения. В области действия этих сил потенциал отрицателен, вне – нулевой.
Энергия частицы Е есть сумма её кинетической энергии Т > 0 и потенциальной U (может быть как положительной, так и отрицательной). Если частица находится внутри ямы, то её кинетическая энергия Т1 меньше глубины ямы U0, энергия частицыЕ1 = Т1 + U1 = Т1 - U0 < 0 и частица не может покинуть яму (находится в связанном состоянии). Она двигается в ней с кинетической энергией Т1, отражаясь от стенок. Если частица находится на дне ямы, то её кинетическая энергия Т2 = 0 и Е2 = -U0 < 0(частица лежит на дне ямы). Это положение частицы наиболее устойчиво. Если частица вне ямы имела кинетическую энергию Т3 то она беспрепятственно пересекает яму, преодолевая её с возросшей кинетической энергией Т3 + U0.
В квантовой механике энергия частицы, находящейся в связанном состоянии, может принимать лишь определённые дискретные значения, т.е. существуют дискретные уровни энергии. При этом наинизший (основной) уровень всегда лежит выше дна ямы. По порядку величины расстояние ΔЕ между уровнями частицы массы m в глубокой яме шириной а даётся выражением ΔЕ  ћ2/mа2.
ћ2/mа2.
Пример потенциальной ямы – ядерная яма глубиной 40- 50 МэВ и шириной 10-13–10-12 см, в которой на различных уровнях находятся нуклоны, двигающиеся со средней кинетической энергией  20 МэВ.
20 МэВ.
На простом примере движения частицы в одномерной бесконечной прямоугольной яме можно легко увидеть, как возникают дискретные значения энергии. В классическом случае частица, двигаясь от одной стенки к другой, принимает любое значение энергии, в зависимости от сообщенного ей импульса. В квантовой системе ситуация совсем другая. Если движение квантовой частицы происходит в ограниченной области пространства, спектр энергий оказывается дискретным.
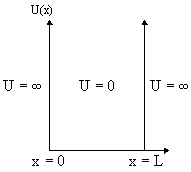 Рис. 2. Бесконечная прямоугольная потенциальная яма. Рис. 2. Бесконечная прямоугольная потенциальная яма.
|
Итак, пусть частица массы m находится в одномерной потенциальной яме бесконечной глубины (рис. 2). Потенциальная энергия U удовлетворяет следующим граничным условиям
 . .
| (1) |
При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е.
| ψ(x) = 0 x < 0, x > L | (2) |
Используя станционарное уравнение Шредингера для случая U = 0, получим
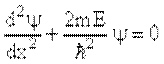
| (3) |
Уравнение (3) описывает положение частицы внутри потенциальной ямы.
Для бесконечной одномерной потенциальной ямы имеем следующее:
1. Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях.  где n = 1, 2, 3...
где n = 1, 2, 3...
2. Частица может находиться в каком-то одном из множества энергетических состояний.
3. Частица не может иметь энергию равную нулю.
4. Каждому значению энергии En соответствует собственная волновая функция ψn, описывающая данное состояние.
5. Для собственной функции ψ1(x) вероятность обнаружить частицу в точке x = L/2 максимальна. Для состояния ψ2(x) вероятность обнаружения частицы в этой точке равна 0 и так далее.
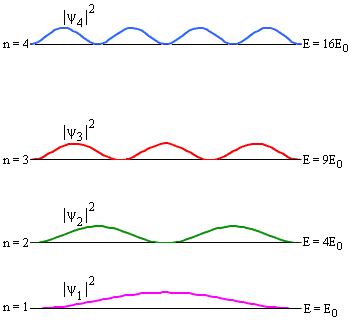 Рис. 2. Плотности вероятности обнаружения частицы в различных квантовых состояниях. Рис. 2. Плотности вероятности обнаружения частицы в различных квантовых состояниях.
|
79. Принцип Паули.
Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Но для фермионов волновая функция должна быть антисимметричной. Отсюда следует, что два одинаковых фермиона, входящих в одну систему не могут находиться в одинаковых состояниях. Обобщая опытные данные, В. Паули сформировал принцип исключения, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантовомеханическая формулировка принципа запрета Паули).
Принцип запрета Паули – фундаментальный закон природы, заключающийся в том, что в квантовой системе две тождественные частицы с полуцелым спином не могут одновременно находиться в одном состоянии. Сформулирован в 1925 г. В.Паули для электронов в атоме и назван им принципом запрета, затем распространен на любые фермионы. В 1940 г. Паули показал, что принцип запрета – следствие существующей в квантовой теории поля связи спина и статистики. Частицы с полуцелым спином подчиняются статистике Ферми – Дирака, поэтому волновая функция системы одинаковых фермионов должна быть антисимметричной относительно перестановки любых двух фермионов; отсюда следует, что в одном состоянии может находиться не более одного фермиона. Принцип Паули сыграл решающую роль в понимании закономерностей заполнения электронных оболочек атома; определяет закономерность распределения электронов в атоме по оболочкам и слоям.
Состояние электрона в атоме характеризуется четырьмя квантовыми числами:
главным  (
( 1, 2, 3, ……);
1, 2, 3, ……);
орбитальным  (
(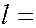 0, 1, 2, …..,
0, 1, 2, …..,  1); всего
1); всего  значений;
значений;
магнитным  (
(
 ….., 0, + 1, ….. +
….., 0, + 1, ….. +  ); всего
); всего 
значение;
спиновым  (
( ); всего 2 значения.
); всего 2 значения.
Распределение электронов в невозбужденном атоме происходит на основе двух принципов:
1. принцип наименьшей энергии: при прочих равных условиях электрон находится в состоянии, при котором его энергия минимальна;
2. принцип запрета Паули, который может быть сформулирован для атома в следующем виде: в одном и том же атоме, не может быть более одного электрона с одинаковым набором четырех квантовых чисел  В соответствии с принципом запрета Паули электроны в атоме распределяются по слоям и оболочкам.
В соответствии с принципом запрета Паули электроны в атоме распределяются по слоям и оболочкам.
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число  , называется электронным слоем (или электронной оболочкой). Максимальное число электронов, находящихся в состояниях, определяемых значением главного квантового числа
, называется электронным слоем (или электронной оболочкой). Максимальное число электронов, находящихся в состояниях, определяемых значением главного квантового числа  (т.е. в слое), равно:
(т.е. в слое), равно: 
Совокупность электронов, имеющих одинаковые значения  и
и  , образуют оболочку (подоболочку). Поскольку орбитальное квантовое число принимает значения от 0 до
, образуют оболочку (подоболочку). Поскольку орбитальное квантовое число принимает значения от 0 до  , число оболочек равно порядковому номеру
, число оболочек равно порядковому номеру  слоя. Количество электронов в облочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным
слоя. Количество электронов в облочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным  равно
равно  . Обозначения слоев, а также распределение электронов по слоям и оболочкам приведены в таблице.
. Обозначения слоев, а также распределение электронов по слоям и оболочкам приведены в таблице.

| |||||||||||||||
| Символ слоя | K | L | M | N | O | ||||||||||
| Максимальное число электронов в слое 2n2 | |||||||||||||||
Орбитальное кв. чис. 
| |||||||||||||||
| Символ оболочки | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
| Максимальное число электронов в оболочке |
Для полностью заполненной оболочки характерно равенство нулю суммарного орбитального и спинового моментов электронов, входящих в оболочку. Поэтому при определении орбитального и спинового моментов атома полностью заполненные оболочки можно не принимать во внимание.
79. Принцип Паули.
Заполнение электронных оболочек в атомах.
1. Принцип Паули: электронов – блуднецов в атомах не бывает, т.е. у атома не может быть 2х электронов с одинаковым набором всех квантовых чисел.
2. При заполнении электронных оболочек необходимо учитывать, что суммарное знание спинового квантового числа в пределах одной подоболочки стремиться с максимальному.
3. Заполнение оболочек осуществляется в соответствии с ростом суммы n+l, при равных значениях этой суммы в первой точке заполняются подоболочки с наименьшим значением n (Клечковский).
S n=2
n=1 1. |↓↑| l=0, ml=0
l=0; ml=0 2. |↓↑|↓↑|↓↑|↓↑| l=1, ml= -1;0;1
n=3 S
l=0, ml=0 1. |x|
l=1, ml= -1;0;1 2. |x|x|x|x|
l=2, ml= -2, -1;0;1,2 3. |x|x|x|x| | | | | | n+l=4+0=4 (4s)
l=3, ml= -3,-2,-1;0;1,2,3 4. |x| | | | n+l=3+2=5 (3d)
Заполнение электронных оболочек в атомах.
| Энергетический уровень, п | Число подуровней, равное n | Орбитали | Число орбиталей | Максимальное число электронов | ||
| в подуровне | в уровне, равное n2 | на подуровне | на уровне | |||
| К (n = 1) | 1s | |||||
| L (n= 2) | 2s 2p | |||||
| М (n= 3) | 3s 3p 3d | 6 10 | ||||
| N (п = 4) | 4s 4p 4d 4f | 6 10 14 |
Порядок заполнения электронами атомных орбиталей определяет принцип наименьшей энергии (принцип минимума энергии):
· Основное (устойчивое) состояние атома — это такое состояние, которое характеризуется минимальной энергией. Поэтому электроны заполняют орбитали в порядке увеличения их энергии.
Сравнить энергии орбиталей можно пользуясь правилами В. Клечковского.
Согласно первому правилу советского ученого В.М. Клечковского (1954 г.), энергия подуровня тем больше, чем больше сумма главного и орбитального квантовых чисел (п+l).
Например: энергия 2s-подуровня больше, чем энергия ls-подуровня, так как для ls-подуровня: п + l= 1 + 0 = 1; для 2s-подуровня: п + l= 2 + 0 = 2; следовательно E2s> Els.
Согласно второму правилу В.М. Клечковского: если для разных подуровней суммы (п + l) одинаковы, то энергия подуровня тем больше, чем больше главное квантовое число (п).
Например: энергия 4р-подуровня больше, чем энергия 3d-подуровня, так как для 4р-подуровня: п + l= 4+1= 5 (n=4); для 3d-подуровня: п +l= 3+ 2 = 5 (n = 3); следовательно Е4p > E3d.
В пределах одного подуровня электроны заполняют свои орбитали согласно правилу Гунда:
На одном подуровне электроны располагаются так, чтобы абсолютное значение суммы спиновых квантовых чисел (суммарного спина) было максимальным. Это соответствует устойчивому состоянию атома.
Например, какое расположение трех электронов на р-подуровне соответствует устойчивому состоянию атома:
1) ¯ ¯ 2) 3) ¯ 4) ¯ ¯ 5) ¯ ¯ ¯
Максимальным абсолютным значением суммарного спина характеризуются состояния 2 и 5. Поэтому именно они соответствуют устойчивым состояниям атома.
Строение атома описывается с помощью схемы электронного строения атома, электронной формулы атома, электронно-графической формулы атома.
Схемы электронного строения атомов показывают распределение электронов по энергетическим уровням.
Например,
Элементы I периода:
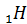 +1)1 ® Схема электронного строения атома Водород
+1)1 ® Схема электронного строения атома Водород
80. Характеристика ядра.
Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12 С:
1а.е.м = 1.6606 10-27 кг.
А.е.м. выражается через энергетические единицы:
1а.е.м = 1.510-3эрг = 1.510-10дж = 931.49 МэВ
Масса покоя частицы m, ее полная энергия E и импульс p связаны соотношением (релятивистский инвариант):
E2 - c2p2 = m2c4. (1.1)
При скорости частицы v = 0 энергия покоя E0 и полная энергия частицы E совпадают
Е0 = mc2 (1.2)
Полная энергия частицы состоит из двух слагаемых:
E = mc2+ T, (1.3)
где Т- кинетическая энергия частицы.
Масса ядра всегда меньше массы составляющих его нуклонов.
Радиус ядра R связан с массовым числом A соотношением
R = r0A1/3, (1.4)
где параметр r0 1.3 Фм.
Энергия связи ядра Eсв(A,Z) это энергия, необходимая, чтобы развалить ядро на отдельные, составляющие его нуклоны. Энергия связи определяется соотношением:
Есв(A, Z) = [Z mp + (A - Z)mn - M(A, Z)] c2,
где Z - число протонов, (A - Z) - число нейтронов, mp - масса протона, mn - масса нейтрона, М(A,Z) - масса ядра с массовым числом А и зарядом Z.
Полная энергия связи ядра, выраженная через массу атома, имеет вид:
Есв(A, Z) = ZmH + (A - Z)mn - Mат(A, Z) - Zme) c2, (1.5)
Удельная энергия связи ядра (A, Z) это энергия связи, приходящаяся на один нуклон
ε(A, Z) = Eсв(A,Z) / A, (1.6)
где А - массовое число.
Избыток масс (дефект масс) связан с массой атома Mат(A,Z) и массовым числом A соотношением:
 = Мат(A,Z) - А, (1.7)
= Мат(A,Z) - А, (1.7)
В таблицах избытки масс атомов даются в энергетических единицах, обычно в кэВ.
Спин ядра J это векторная сумма спинов и орбитальных моментов составляющих ядро нуклонов.
 ,
,
где  i - спины составляющих ядро нуклонов,
i - спины составляющих ядро нуклонов,  i - их орбитальные моменты.
i - их орбитальные моменты.
Четность ядра P определяется орбитальными моментами составляющих его нуклонов
 . (1.8)
. (1.8)
На рисунке показана типичная схема уровней (ядро 12C). Указаны энергии возбуждения в МэВ, а также спины и четности состояний. Минимальное значение энергии покоя (массы) имеет ядро, находящееся в состоянии, когда энергия внутреннего движения нуклонов минимальна. Такое состояние называется основным. Энергия возбуждения отсчитывается от основного состояния. На рисунке показаны также основные состояния ядер 12B и 12N, распадающиеся в результате β− и β+-распадов на основное и возбужденные состояния ядра 12C.

Рис. 1. Схема уровней ядра 12С.
80. Характеристика ядра.
Состав ядра. Экспериментально установлено, что атомное ядро состоит из протонов и нейтронов. Эти частицы называют нуклонами.
Протон (р) обладает положительным зарядом е и массой

где mе — масса электрона, а.е.м. — атомная единица массы. Значение массы протона приведено в энергетических единицах как принято в ядерной физике.
Протон имеет спин s = 1/2 и собственный магнитный момент


где mя — ядерный магнетон (единица, в которой измеряют магнитные моменты нуклонов):
Ядерный магнетон в 1836 раз меньше магнетона Бора, т. е. собственный магнитный момент протона в 660 раз меньше магнитного момента электрона.

Нейтрон (n). Его электрический заряд равен нулю, а масса близка к массе протона: что на 0,14% или 2,5 mе больше массы протона.
Атомная единица массы равна 1/12 массы нейтрального атома 12С, т. е. 1 а.е.м. = 1,66·10-24 г или 931,50 МэВ.
Спин нейтрона s = 1/2 и, несмотря на отсутствие электрического заряда, нейтрон имеет магнитный момент
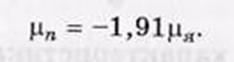
Знак минус означает, что «направления» спина и магнитного момента у нейтрона взаимно противоположны.
В свободном состоянии нейтрон нестабилен и самопроизвольно распадается, превращаясь в протон и испуская электрон и еще одну частицу, нейтрино (v):

Период полураспада (время, за которое распадается половина первоначального количества нейтронов) равно примерно 12 мин.
Характеристики атомного ядра. Основными величинами, характеризующими атомное ядро, являются зарядовое Z и массовое А числа. Число Z равно количеству протонов в ядре и определяет его электрический заряд Ze. Его также называют атомным номером. Массовое число А определяет число нуклонов в ядре. Число нейтронов в ядре
N = А - Z.
Символически эти характеристики ядра обозначают так:

где под X имеется в виду химический символ элемента, которому принадлежит данное ядро, например,  Н,
Н,  Hе,
Hе, 
 U и т. д.
U и т. д.
Конкретные атомы с данным числом протонов и нейтронов в ядре принято называть нуклидами. Нуклиды с одинаковым числом протонов (т. е. принадлежащие одному химическому элементу) называют изотопами.
Атомы изотопов обладают практически очень близкими физико-химическими свойствами. Это связано с тем, что на строение электронной оболочки атома ядро влияет в основном только своим электрическим полем. У изотопов эти поля одинаковы, за исключением некоторых случаев. Сильнее всего это различие у трех нуклидов:  Н,
Н,  Н и
Н и  H, ядра которых также существенно отличаются друг от друга. Поэтому этим трем нуклидам присвоены разные названия — соответственно обычный водород, дейтерий и тритий, а ядра дейтерия и трития — дейтрон (d) и тритон (t).
H, ядра которых также существенно отличаются друг от друга. Поэтому этим трем нуклидам присвоены разные названия — соответственно обычный водород, дейтерий и тритий, а ядра дейтерия и трития — дейтрон (d) и тритон (t).
У разных атомов число изотопов различно, среди них имеются стабильные и радиоактивные.
Размеры ядер. У атомного ядра (как и у всякой квантовой системы) нет четко определенной границы. В экспериментах по рассеянию электронов и нуклонов на ядрах установлено, что в каждом ядре имеется внутренняя область, в которой плотность ρ ядерного вещества практически постоянна, и
поверхностный слой, где эта плотность падает до нуля. Типичное распределение концентрации нуклонов в зависимости от расстояния до центра
ядра, т. е. п (г) показано на рисунке
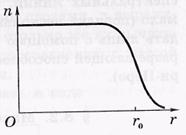
где r о — радиус ядра — расстояние от центра ядра, на котором концентрация нуклонов падает в два раза.
В первом приближении ядро можно считать сферическим радиуса

где 1 фм = 10-13 см. Из этой формулы вытекает важный вывод: масса ядра, определяемая массовым числом А, пропорциональна его объему V, поскольку V ~ г  ~ А. Следовательно, плотность вещества во всех ядрах примерно одинакова и, как показывает расчет, равна ρ
~ А. Следовательно, плотность вещества во всех ядрах примерно одинакова и, как показывает расчет, равна ρ  2·1014 г/см3.
2·1014 г/см3.
Масса и энергия связи ядра
Масса ядра не является аддитивной величиной: она не равна сумме масс образующих ядро нуклонов. Причиной является сильное взаимодействие нуклонов в ядре. Из-за этого взаимодействия для полного разделения ядра на отдельные свободные нуклоны необходимо произвести минимальную работу, которая и определяет энергию связи ядра Есв. Наоборот, при образовании ядра из свободных нуклонов эта энергия выделяется (в виде, например, электромагнитного излучения).
Энергия связи, дефект масс.
Исследования показывают, что атомные ядра являются устойчивыми образованиями. Это означает, что в ядре между нуклонами существует определенная связь. Изучение этой связи может быть проведено без привлечения сведений о характере и свойствах ядерных сил, а основываясь на законе сохранения энергии. Введём определения.
Энергией связи нуклона в ядре называется физическая величина, равная работе, которую необходимо совершить для удаления данного нуклона из ядра без сообщения ему кинетической энергии.
Полная энергия связи ядра определяется работой, которую нужно совершить для расщепления ядра на составляющие его нуклоны без придания им кинетической энергии.
Из закона сохранения энергии следует, что при образовании ядра из составляющих его нуклонов должна выделиться энергия, равная энергии связи ядра. Очевидно, что энергия связи ядра равна разности между суммарной энергией свободных нуклонов, составляющих данное ядро, и их энергией в ядре. Из теории относительности известно, что между энергией и массой имеется связь:
Е = mс2. (250)
Если через ΔЕсв обозначить энергию, выделяющуюся при образовании ядра, то с этим выделением энергии, согласно формуле (250), должно быть связано уменьшение суммарной массы ядра при его образовании из составных частиц:
Δm = ΔЕсв / с2 (251)
Если обозначить через mp, mn, mЯ соответственно массы протона, нейтрона и ядра, то Δm можно определить по формуле:
Dm = [ Zmр + (A-Z)mn ] - mЯ . (252)
Массу ядер очень точно можно определить с помощью масс-спектрометров - измерительных приборов, разделяющих с помощью электрических и магнитных полей пучки заряженных частиц (обычно ионов) с разными удельными зарядами q/m. Масс-спектрометрические измерения показали, что, действительно, масса ядра меньше, чем сумма масс составляющих его нуклонов.
Разность между сумой масс нуклонов, составляющих ядро, и массой ядра называется дефектом массы ядра (формула (252)).
Согласно формуле (251), энергия связи нуклонов в ядре определится выражением:
ΔЕСВ = [ Zmp + (A-Z) mn – mЯ ] с 2. (253)
В таблицах обычно приводятся не массы ядер mЯ, а массы атомов mа. Поэтому для энергии связи пользуются формулой
ΔЕСВ = [ ZmH + (A-Z) mn – mа ] с 2 (254)
где mH - масса атома водорода 1Н1. Так как mH больше mр, на величину массы электрона me, то первый член в квадратных скобках включает в себя массу Z электронов. Но, так как масса атома mа отличается от массы ядра mЯ как раз на массу Z электронов, то вычисления по формулам (253) и (254) приводят к одинаковым результатам.
Часто вместо энергии связи ядра рассматривают удельную энергию связи dЕСВ - это энергия связи, приходящаяся на один нуклон ядра. Она характеризует устойчивость (прочность) атомных ядер, т. е. чем больше dЕСВ,тем устойчивее ядро. Удельная энергия связи зависит от массового числа А элемента. Для легких ядер (А £ 12) удельная энергия связи круто возрастает до 6 ¸ 7 МэВ, претерпевая целый ряд скачков (см. рисунок 93). Например, для  dЕСВ =1,1 МэВ, для
dЕСВ =1,1 МэВ, для  -7,1 МэВ, для
-7,1 МэВ, для  -5,3 МэВ. При дальнейшем увеличении массового числа dЕСВ возрастает более медленно до максимальной величины 8,7 МэВ у элементов с А =50¸60, а потом постепенно уменьшается для тяжелых элементов. Например, для
-5,3 МэВ. При дальнейшем увеличении массового числа dЕСВ возрастает более медленно до максимальной величины 8,7 МэВ у элементов с А =50¸60, а потом постепенно уменьшается для тяжелых элементов. Например, для  она составляет 7,6 МэВ. Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (в 106 раз меньше). На кривой зависимости удельной энергии связи от массового числа для стабильных ядер (рисунок 93) можно отметить следующие закономерности:
она составляет 7,6 МэВ. Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (в 106 раз меньше). На кривой зависимости удельной энергии связи от массового числа для стабильных ядер (рисунок 93) можно отметить следующие закономерности:
 а) Если отбросить самые легкие ядра, то в грубом, так сказать нулевом приближении, удельная энергия связи постоянна и равна примерно 8 МэВ на
а) Если отбросить самые легкие ядра, то в грубом, так сказать нулевом приближении, удельная энергия связи постоянна и равна примерно 8 МэВ на
нуклон. Приближенная независимость удельной энергии связи от числа нуклонов свидетельствует о свойстве насыщения ядерных сил. Это свойство состоит в том, что каждый нуклон может взаимодействовать только с несколькими соседними нуклонами.
б) Удельная энергия связи не строго постоянна, а имеет максимум (~8,7 МэВ/нуклон) при А = 56, т.е. в области ядер железа, и спадает к обоим краям. Максимум кривой соответствует наиболее стабильным ядрам. Легчайшим ядрам энергетически выгодно сливаться друг с другом с выделением термоядерной энергии. Для наиболее тяжелых ядер, наоборот, выгоден процесс деления на осколки, идущий с выделением энергии, получившей название атомной.
Наиболее устойчивыми оказываются так называемые магические ядра, у которых число протонов или число нейтронов равно одному из магических чисел: 2, 8, 20, 28, 50, 82, 126. Особенно стабильны дважды магические ядра, у которых магическими являются и число протонов, и число нейтронов. Этих ядер насчитывается всего пять:  ,
,  ,
,  ,
,  ,
, 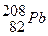 .
.
81.Типы радиоактивных распадов.
Нуклид является стабильным в отношении радиоактивного распада, если его масса меньше суммы масс всех продуктов, образующихся при предполагаемом распаде. Поэтому радиоактивный распад возможен только в том случае, если сумма масс образующихся продуктов будет меньше массы исходного нуклида. Радиоактивный распад в общем виде можно представить следующим образом:
А (материнский нуклид) = В(дочерний нуклид) + Х (испускаемые частицы) + Q(энергия)
Под энергией подразумевают кинетическую энергию испускаемых частиц и g-квантов. Суммарная энергия Q, выделяющаяся при радиоактивном распаде, определяется разностью масс исходного нуклида и продуктов, образующихся после распада в основном состоянии:
Q=dmc2=(mA-mB-mX)c2.
Во всех случаях радиоактивного распада соблюдаются законы сохранения массы и заряда.
По типу испускаемых частиц различают следующие виды радиоактивного распада:
1) a-распад;
2) b-распад, который подразделяется на b--распад, b+-распад и электронный захват (ЭЗ);
3) эмиссия 7-квантов, электронов конверсии и электронов Оже;
4) спонтанное деление.
Альфа-распад. Альфа-распаду подвержены ядра многих изотопов (тяжёлых) элементов − урана, радия, тория и др. Возможность α-распада связана с тем, что масса (а значит, и энергия покоя) α-радиоактивного ядра больше суммы масс (суммарной энергии покоя) α-частицы и образующего после α-распада дочернего ядра. Избыток энергии исходного (материнского) ядра освобождается в форме кинетической энергии α-частицы и дочернего ядра. Кинетическая энергия α-частиц у большинства α-радиоактивных ядер находится в небольших пределах 4 − 9 Мэв. Периоды полураспада, наоборот, изменяются очень сильно: от 10-7 сек до 2∙1017 лет.
Бета-распад. В процессе β-распада из радиоактивного ядра самопроизвольно испускается электрон (электронный β-распад) или позитрон (позитронный β-распад), которые возникают в самый момент β-распада (их нет в ядре). Третьим видом β-распада является захват ядром электрона из электронной оболочки своего атома (е-захват). Во всех трёх случаях β-распад сопровождается испусканием нейтрино или антинейтрино. В результате β-распада заряд ядра повышается, β+-распада и е-захвата понижается на единицу. Массовое число ядра остаётся неизменным.
Электронный распад испытывают ядра с избытком нейтронов. Этому типу распада подвержены почти все искусственные и некоторые естественные радиоактивные элементы (С12, К40 и др.)
При электронном распаде вновь образующееся дочернее ядро сохраняет массовое число исходного элемента, а положительный заряд нового ядра в результате превращения нейтрона в протон оказывается на одну единицу больше заряда ядра исходного элемента.
Материнский и дочерний радионуклиды при электронном распаде представляют собой изобары, так как сумма протонов и нейтронов не изменяется.
Позитронный распад испытывают ядра с избытком протонов. Этому типу распада подвержены лишь некоторые искусственные радиоактивные изотопы, например 6С11, в ядре которого при 5 нейтронах содержится 6 протонов. У естественных радиоактивных изотопов позитронный распад не наблюдается.
Электронный захват. Радиоактивные изотопы избавляются от избыточных протонов путём электронного захвата, который наблюдается в случае, когда в ядре недостаточно энергии для позитронного распада. Такое ядро обычно захватывает электроны (е-захват) с ближайшего слоя (К-слоя, иногда L-слоя) и «лишний» протон, соединившись с эти электроном, превращается в нейтрон, испуская нейтрино. Следовательно, е-захват представляет собой процесс, прямо противоположный электронному распаду. В данном случае дочерний элемент так же, как и при позитронном распаде, смещается в периодической системе на одну клетку влево от исходного. На освободившееся в К-слое место перескакивает электрон с L-слоя, на место последнего с М-слоя и т.д. каждый перескок связан с высвобождением энергии, которая и высвечивается с квантами рентгеновского излучения.
Гамма-лучи представляют собой поток γ-квантов, т.е. коротковолновых электромагнитных излучений, испускаемых возбуждёнными атомными ядрами.
В процессе γ-излучения ядро самопроизвольно переходит из возбуждённого состояния в менее возбуждённое или основное. При этом избыток энергии освобождается в виде кванта коротковолнового электромагнитного излучения − γ-кванта. γ-кванты лишены заряда и поэтому не отклоняются электрическим или магнитным полем. Они распространяются прямолинейно и равномерно во все стороны от источника.
В большинстве случаев γ-источники испускают γ-кванты различной энергии, т.е. они бывают моноэнергетическими. Нуклиды, находящиеся в возбужденном состоянии, могут распадаться, испуская нейтроны или протоны.
Радионуклиды претерпевают самопроизвольный распад и становятся источниками излучений определенного вида и строго определенной для каждого атома энергии. Различают несколько основных типов радиоактивного распада и соответствующие им виды излучения.
1) Альфа (a)-излучение представляет собой поток ядер атомов гелия (два протона + два нейтрона). Возникает оно в результате альфа-распада, который характерен для радиоактивных изотопов с большим атомным номером. Испускание a-частицы приводит к образованию нового химического элемента, у которого заряд ядра меньше на две единицы и массовое число – меньше на четыре единицы.
2) Бета (b)-излучение представляет собой поток электронов или позитронов. Возникает оно в результате бета-распада ядра атома. Если в ядре есть избыток нейтронов, то один из них распадается с образованием протона, который остается в ядре, электрона, который испускается в виде бета-излучения, а также антинейтрино, не имеющего ни массы, ни заряда, но уносящего из ядра часть энергии. Антинейтрино очень трудно обнаружить, так как оно практически не взаимодействует с веществом.
Позитрон - античастица электрона образуется при распаде ядра с избытком протонов. Такой тип распада встречается гораздо реже, чем b-распад.
3) Гамма (g)-излучение представляет собой поток фотонов или квантов электромагнитного излучения. При наличии в ядре избытка энергии, например, после a- или b-распада, переход ядра из возбужденного состояния в стабильное может происходить путем гамма-изомерного перехода, т.е. с испусканием гамма-квантов. При этом атомный номер элемента и массовое число изотопа остаются прежними, меняется только энергетическое состояние ядра.
Наряду с понятием «ионизирующее излучение» используется термин «радиация». Эти понятия одинаковы по смыслу и являются синонимами.
Энергия излучения, выделяющаяся при радиоактивном распаде ядра атома, несоизмеримо больше энергии обычных химических реакций, которые протекают путем взаимодействия между орбитальными электронами атомов. Единицей измерения энергии ядерных изменений является электрон-вольт (эВ). 1 эВ = 1,6×10-19 Дж.
Date: 2016-07-22; view: 2555; Нарушение авторских прав