Приближенные математические модели технических объектов на микроуровне

Точные решения дифференциальных краевых задач удается получить лишь для немногих частных случаев. Проектирование технических объектов на микроуровне осуществляют на основе приближенных математических моделей, получаемых путем аппроксимации исходных моделей. Так же поступают и при решении большинства исследовательских задач. Аппроксимация осуществляется посредством дискретизации и алгебраизации дифференциальной краевой задачи.

Дискретизация представляет собой замену областей непрерывного изменения пространственных координат , , и времени t дискретным множеством точек. Эти точки называют узлами сетки и в них определяют искомые значения фазовой переменной . В этом случае непрерывная функция заменяется множеством ее значений в узлах сетки. В результате функция и все ее аргументы оказываются дискретизированными.

Используя значения функции в узлах сетки, можно через них приближенно выразить частные производные дифференциальных уравнений, описывающих исследуемый процесс технического объекта и краевые условия. Тогда дифференциальные уравнения в частных производных преобразуются в алгебраические уравнения. В этом заключается суть алгебраизации дифференциальной краевой задачи.

Приближенные математические модели технических объектов на микроуровне получают на основе методов сеток.

В зависимости от способов осуществления дискретизации и алгебраизации краевых задач различают два метода сеток: метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Рассмотрим основные особенности этих методов.

Напомним, что технический объект на микроуровне представляет собой сплошную среду, локализуемую в некоторой ограниченной области Н геометрического пространства, определяемой вектором координат , т.е. . Координаты геометрического пространства в дальнейшем будем обозначать х, у,z, тогда .(стр53)

В МКР дискретизация задачи заключается в покрытии области сеткой и замене непрерывного множества независимых переменных в области конечным множеством точек являющихся узлами сетки. Сетка может быть прямоугольной, косоугольной, с постоянными или переменными расстояниями

Рис. 2.2. Дискретизация области определения

объекта моделирования с помощью сетки (а)

и аппроксимация границы области (б)

между узлами (шагами сетки). Наиболее часто используют сетку с постоянными величинами шагов. Такую сетку называют регулярной. На рис. 2.2, а показан пример построения сетки для двумерного объекта. Шаги сетки вдоль координатных соей х и у обозначены соответственно и . Узлы сетки, попавшие внутрь области , называются внутренними. Точки пересечения прямых, образующих сетку, с границей S области называются граничными узлами.

Алгебраизация задачи в МКР выполняется путем замены дифференциального оператора уравнения (2.2) разностным. При этом частные производные аппроксимируют отношениями конечных разностей, выражаемых через конечное множество значений функции в узлах сетки. В нестационарной задаче, когда зависит не только от геометрических координат, но и от времени t, т.е. , дискретизации подлежит также независимая переменная t.

При использовании МКР возникают сложности в обеспечении точности математического описания граничных условий. В общем случае геометрическая область определения объекта Е может иметь сложную форму границы S. Тогда граничные узлы отстоят от ближайших к ним внутренних узлов на расстояния, меньше шага сетки (рис. 2.2, б). Это приводит к необходимости либо отказа от регулярной сетки, либо замены действительной линии образующей граничной поверхности S ломаной линией S'. В любом варианте значительно осложняется моделирование технического объекта.

Метод конечных разностей. Представим дифференциальное уравнение (2.2) в следующем виде:

(2.61)

где — вектор геометрических координат: .

Дифференциальный оператор может включать первые, вторые, третьи и т.д. производные функции ср по независимым переменным х, у,z. Эти производные при алгебраизации задачи заменяются отношениями конечных разностей.

Выполним алгебраизацию уравнения (2.61), полагая, что технический объект одномерный и моделируемый процесс стационарный, т.е . Предположим, что дифференциальный оператор . Тогда исходное дифференциальное уравнение имеет вид .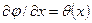

Осуществим дискретизацию независимой переменной х, введя сетку с постоянным шагом h, и заменим частную производную следующим отношением конечной разности:

(2.62)

Подставляя выражение (2.62) в исходное дифференциальное уравнение, получаем разностное уравнение

(2.63)

Пронумеруем узлы сетки от 0 до n+1. Узлы с номерами 0 и n+1 будут граничными, а узлы — внутренними. В результате дискретизации независимой переменной х она получает следующие значения в узлах сетки: . Подставляя последовательно эти значения в уравнение (2.63), получаем систему алгебраических уравнений:

(2.64)

В системе уравнений (2.64) при х=0, h, 2h,... — заданная функция, определяемая в узлах сетки, а и — значения фазовой переменной ф в граничных узлах, определяемые из уравнений, описывающих граничные условия. Если граничные условия описываются дифференциальными уравнениями в частных производных, то для определения и

они также должны быть подвергнуты конечно-разностной аппроксимации.

Решив систему алгебраических уравнений совместно с разностными уравнениями граничных условий, найдем дискретный ряд значений функции ф во всех внутренних узлах сетки, т.е.значения . Чем меньше шаг сетки h, тем точнее результаты определения функции по приближенной математической модели (2.64). Однако при этом увеличивается размерность системы уравнений и возрастают затраты времени на получение решения.

Аппроксимация частной производной выражением (2.62) не единственная. Существуют и другие конечно-разностные выражения. При аппроксимации производных удобно пользовать-ся шаблонами, приведенными на рис. 2.3. Шаблоны на рис. 2.3, а — г используются для' одномерных задач, а на рис. 2.3, д — ж — для двумерных. Шаблон представляет собой часть сетки, включающую множество узлов значения переменных в которых используются при аппроксимации производных в заданном узле X. Узлы на рис. 2.3 показаны кружками, а узел X обведен дополнительной окружностью. Слева от шаблонов указан аппроксимируемый дифференциальный оператор, а рядом с узлами сетки записаны значения коэффициентов, с которыми соответствующие величины входят в конечноразностные выражения.

Направления осей координат на рис. 2.3 выбраны таким образом, чтобы полученные результаты вычислений функции в таблице, напечатанной на принтере, располагались в порядке следования узлов сетки.

Шаблоны, показанные на рис. 2.3, а, б, в, позволяют составить выражения соответственно правой, левой и центральной конечно-разностных аппроксимаций производной :

(2.65)

(2.66)

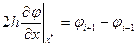(2.67)

Для второй производной, согласно рис. 2.3, г, получаем

(2.68)

В выражениях (2.65) — (2.68) индекс iпри искомой переменной соответствует номеру узла сетки.

Шаблоны, показанные на рис. 2.3, д — ж, используются при решении двумерных задач. Сетка в этом случае разделяет объект на вертикальные слои вдоль координаты х и на горизонтальные слои вдоль координаты у, отделяя слои друг от друга соответствующими плоскостями (вертикальными и горизонтальными). Координаты этих плоскостей обозначены соответственно и , где i и j — номера плоскостей. Узлы

сетки находятся на пересечениях вертикальных и горизонтальных плоскостей, а их расположение на координатной плоскости хОу определяется двумя координатами: по оси х и по оси у.

В результате искомая переменная должна иметь двойной индекс. Например, значение , соответствующее узлу сетки с координатами х₁₊₁ и , обозначается Принимая сетку с шагами , составим конечно-разностные аппроксимации дифференциальных операторов, шаблоны для которых приведены на рис. 2.3, д — ж:

(2.69)

(2.70)

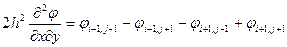(2.71)

где — оператор Лапласа (в двумерной задаче

)

Подстановка выбранных аппроксимаций производных в исходное уравнение (2.61) и в уравнения граничных условий преобразует их для стационарной задачи в систему разностных уравнений

(2.72)

а для нестационарной — в систему обыкновенных дифференциальных уравнений (2.73)

где — вектор, элементами которого являются значения фазовой переменной во внутренних узлах сетки.

Традиционно МКР применяют при моделировании движения жидкостей и газов в трубопроводах и теплообменных процессов. Рассмотрим примеры применения МКР для моделирования теплопередачи в одномерных и двумерных теплотехнических объектах.

Пример 2.1. Аппроксимировать исходную математическую модель одномерного теплового объекта при стационарной теплопередаче, полагая отсутствие в нем внутренних источников.

Согласно выражению (2.19), дифференциальное уравнение теплопроводности в этом случае .

Если объектом является изотропное тело, для всей области . Применяя регулярную сетку 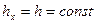и используя выражение (2.68), получаем систему разностных уравнений

(2.74)

Если объект представляет собой стержень постоянного сечения и состоит из участков, изготовленных из материалов, различающихся физическими свойствами, то для аппроксимации частной производной необходимо использовать следующее конечно-разностное отношение:

Математическая модель теплопередачи в этом случае должна также учитывать различие коэффициента температуропроводности для участков стержня. В результате получаем

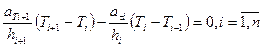
Введем обозначение и выполним приведение подобных:

(2.75)

Очевидно, что уравнение (2.74) является частным случаем уравнения

(2.75) при 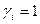. Используя (2.75), составим разностные уравнения для всех внутренних узлов , перенеся в правые их части значения функции Т в граничных узлах:

(2.76)

Уравнения (2.76) можно записать в матричной форме , (2.77) где А — матрица коэффициентов системы алгебраических уравнений (2.76), называемая матрицей Якоби; 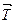— вектор искомых значений функции; — вектор внешних воздействий, определяемый заданными краевыми условиями. Выпишем матрицу А системы уравнений (2.76):

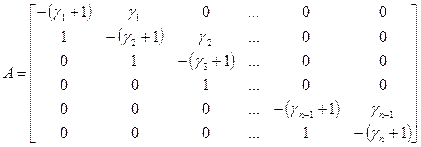(2.78)

Матрица А оказалась ленточной трехдиагональной. Это объясняется тем, что в данном случае при аппроксимации частной производной использовался трехточечный шаблон согласно рис. 2.3, г. В результате в каждом уравнении сио-темы (2.76) фигурируют не более трех неизвестных.

Для определения значений функции Т в граничных точках, т.е. Т₀ и ,

необходимо использовать уравнения граничных условий. Рассмотрим решение задачи для двух вариантов граничных условий: первого рода и третьего рода при конвективном теплообмене с окружающей средой.

Граничные условия первого рода описываются выражением (2.22). В одномерном случае при стационарной теплопередаче задаются значения и 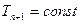, которые непосредственно подставляются в уравнения (2.76).

Граничные условия третьего рода при конвективном теплообмене описываются выражением (2.26). В одномерном случае для левой и правой граничных поверхностей получаем следующие выражения:

(2.79)

где и — коэффициенты теплопроводности левого и правого граничных слоев; и — коэффициенты теплообмена через конвекцию на левой и пра-вой граничных поверхностях; Т_с1 и Т_с2 — температуры окружающих сред на ле-вой и правой границах; b — размер объекта по оси х (длина стержня).

Предположим, что Т_с1 > Т_с2. Тогда градиент температуры в левом граничном слое будет отрицательным, а в правом — положительным. Учитывая это и используя выражение конечно-разностной аппроксимации (2.65), получаем

Из этих выражений находим

(2.80)

(2.81)

Значения функции Т в граничных узлах, определяемые выражениями (2.80) и (2.81), необходимо подставить в систему уравнений (2.76). Решение этой системы позволяет получить искомые значения температуры во всех внутренних узлах объекта.

Для решения системы алгебраических уравнений с трехдиагональной матрицей коэффициентов разработан и широко применяется весьма эффективный метод, называемый методом прогонки. Этот метод рассматривается в разделе 8.11.

В одномерной нестационарной задаче уравнение теплопроводности имеет вид . МКР преобразует это уравнение в систему обыкновенных дифференциальных уравнений.

В заключение отметим, что математические модели одномерных объектов микроуровня посредством конечно-разностной аппроксимации частных производных искомых функций по геометрическим координатам можно легко привести к моделям макроуровня, что будет показано в главе 3 для объектов различной физической природы, а также в разделе 5.7 при моделировании теплопередачи в твердых телах.

Пример 2.2. Аппроксимировать исходную математическую модель двумерного теплового объекта.

Рис. 2.4. Схема к примеру 2.2

Пусть объект представляет собой изотропное тело прямоугольной

формы (рис. 2.4), в котором отсутствуют внутренние источники , а внешние воздействия стационарны. Тогда и в соответствии с (2.17) и (2.18) уравнение теплопроводности имеет вид

(2.82)

При дискретизации объекта используем прямоугольную

сетку с шагами h _х и h у вдоль осей координат х и у. Если , тогда аппроксимацию производных уравнения (2.82) по шаблону на рис. 2.3, г необходимо выполнять раздельно вдоль каждой из координатных осей. Для конечно-разностного выражения, аппроксимирующего , используем узлы, расположенные в вертикальной плоскости при , а для — в горизонтальной плоскости при

Подставим эти выражения в уравнение (2.82):

(2.83)

;

где — для изотропного тела или — для анизотропного тела при : n и m— количества рядов внутренних узлов сетки соответственно вдоль осей х и у (на рис. 2.4 n=4, m=7).

Порядок полученной системы алгебраических уравнений (2.83) равен . Очевидно, что он значительно выше, чем для одномерной задачи. Еще более высокий порядок системы получается для трехмерных объектов, что требует огромных вычислительных затрат при решении подобных задач.

Используя выражения (2.83), составим уравнения для всех узлов с номерами при i = 1, перенося при этом в правые части уравнений значения функции Т, соответствующие граничным узлам:

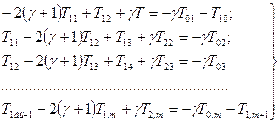(2.84)

где — значения функции Т в граничных узлах, соответствующих х=0; Т₁₀ — значение функции Т в граничном узле с координатами — то же в узле с координатами .

Для узлов с номерами при i = 2 получаем

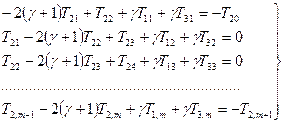(2.85)

где T₂₀ — значение Т в узле с координатами х = 2h_Х; у = 0; — то же в узле с координатами ; .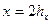

Остальные уравнения составляются аналогично. Количество таких систем уравнений равно п.

Для решения системы алгебраических уравнений (2.83) уравнения (2.84), (2.85) и др. необходимо привести к виду (2.77), т.е. заменить матрицу искомых функций 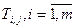(двумерный массив), вектором . Это преобразование выполняется на основе выражения

. (2.86)

Матрица коэффициентов системы уравнений (2.77) для двумерной задачи имеет вид

(2.87)

В матрице А использовано обозначение .

Матрица А в данном случае оказалась пятидиагональной. Это обусловлено тем, что аппроксимация производных выполнялась по пятиточечному шаблону. Причем, диагонали с элементами 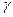отстоят от главной диагонали на столбцов. Кроме того, через каждые т элементов, отсчитываемых по главной диагонали, элементы двух смежных диагоналей оказываются равными нулю, в то время как остальные элементы этих диагоналей равны единице.

Вектор правых частей системы уравнений (2.77) имеет такую же размерность, как и вектор искомых функций 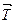. Формирование вектора нетрудно проследить на основе уравнений (2.84) и (2.85).

Для решения системы алгебраических уравнений (2.77) с пятидиагональной матрицей коэффициентов А используется метод матричной прогонки [19].

Date: 2016-07-18; view: 971; Нарушение авторских прав