Основы построения математических моделей на микроуровне

Для построения математических моделей технических объектов с распределенными параметрами используют фундаментальные физические законы. К ним относятся, прежде всего, за коны сохранения (массы, энергии, количества движения).

Общая формулировка закона сохранения: изменение во времени некоторой субстанции в элементарном объеме равно сумме притока-стока этой субстанции через его поверхность с учетом скорости генерации или уничтожения субстанции в этом объеме.

Уравнение, соответствующее данной формулировке, имеет вид

(2.3)

где — фазовая переменная (координата), выражающая субстанцию; — вектор плотности потока фазовой переменной; — дивергенция вектора ; G— скорость генерации или уничтожения субстанции.

У трехмерного технического объекта вектор состоит из трех составляющих, направленных параллельно осям декартовой системы координат т.е. . Дивергенция вектора — скалярная величина, определяемая выражением

(2.4)

Дивергенция вектора плотности потока характеризует сумму притока-стока субстанции через поверхность элементарного объема. В качестве субстанции в различных физических законах выступают: масса, энергия, количество движения и др.

Уравнение закона сохранения массы

, (2.5)

где — плотность массы, кг/м³; — вектор плотности потока массы:

; (2.6)

— вектор скорости переноса массы.

Уравнение (2.5) в гидроаэродинамике называют уравнением неразрывности.

В одномерном случае, когда скорость направлена лишь вдоль оси х, уравнение (2.5) имеет вид

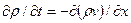(2.7)

Плотность потока массы измеряется в кг/(м²-с).

Уравнение закона сохранения энергии

, (2.8)

где — полная энергия единицы массы; е — внутрен-няя энергия единицы массы; — энергия единицы объема, Дж/м³; — вектор плотности потока энергии; — скорость генерации или поглощения энергии в единице объема, Дж/(м³-с).

В одномерном случае поток энергии направлен только вдоль оси х, тогда , а уравнение (2.8) принимает вид

(2.9)

Плотность потока энергии измеряется в Дж/(м²-с).

Уравнение закона сохранения количества движения используют при моделировании движения потока жидкости. Для потока идеальной жидкости (без учета сил трения, обусловленных вязкостью) уравнение имеет вид

(2.10)

где — вектор количества движения единицы объема жидкости; р — давление жидкости; — градиент давления.

Градиентом называют векторную функцию скалярного аргумента. Компонентами вектора градиента являются частные производные аргумента по пространственным координатам. Градиент давления .

Для одномерного потока жидкости получаем

(2.11)

При учете массовых сил и сил трения уравнение закона сохранения количества движения имеет вид

(2.12),

где — напряженность поля массовых сил; т)—динамическая вязкость; — оператор Лапласа:

Выражение (2.12) называют уравнением Навье — Стокса.

Уравнения математических моделей микроуровня объектов другой физической природы можно найти в литературных источниках, например в [7,19].

Date: 2016-07-18; view: 491; Нарушение авторских прав