Объекты проектирования на микроуровне

Микроуровенъ — это нижний иерархический уровень декомпозиции объектов проектирования по степени абстрагирования при составлении математического описания. На этом уровне осуществляется детальное описание физических свойств технического объекта. Объекты рассматриваются как сплошные среды, имеющие конечные области определения, выделяемые в трехмерном геометрическом пространстве. Такие объекты представляют собой динамические системы с распределенными параметрами. Их также называют непрерывными системами. Функционирование этих систем описывается дифференциальными уравнениями в частных производных.

Общий вид уравнений математической модели описания физических свойств технического объекта с распределенными параметрами

(2.1)

или в компактной форме (2.2)

где — дифференциальный оператор; — искомая функция (фазовая координата); — пространственные координаты; п — количество пространственных координат; t — время; — вектор независимых переменных; — известная функция независимых координат.

Независимыми переменными в этих моделях являются пространственные координаты 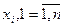, и время t. Фазовая координата — функция независимых переменных.

Размерность задачи определяется числом пространственных координат п: при п = 1 — объект одномерный; при п = 2 — двумерный; при п = 3 — трехмерный.

Если уравнение содержит одну фазовую переменную, система описывается одним уравнением вида (2.1), если несколько фазовых переменных, т.е. вектор , то системой уравнений.

Если фазовые переменные не являются явными функциями времени, задачу анализа объекта называют стационарной, в противном случае — нестационарной. Стационарная задача характеризует статическое состояние технического объекта. Динамические режимы. функционирования объекта относятся к нестационарным задачам и для их оценки требуются исследования переходных процессов.

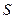Уравнение (2.1) имеет множество решений. Для получения единственного решения необходимо задать краевые условия. Краевые условия включают граничные и начальные условия. Граничные условия — это сведения об искомых непрерывных функциях и (или) их производных на границе области определения объекта , характеризующие условия взаимодействия с окружающей внешней средой. Начальные условия — это значения этих же функций во всей области определения в начальный момент времени. Начальные условия задаются только при решении нестационарных задач (при исследовании переходных процессов).

Исходное дифференциальное уравнение в частных производных (2.1) вместе с краевыми условиями носит название дифференциальной краевой задачи и представляет собой математическую модель технического объекта с распределенными параметрами.

Существует несколько стандартных способов задания граничных условий. Для теплового объекта, представляющего собой твердое гомогенное (однородное) тело, используют граничные условия первого, второго и третьего родов.

Граничные условия первого рода означают задание на границе 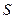области определения объекта значений искомой функции фазовой переменной .

При граничных условиях второго рода задают на границе значения частных производных искомой функции по пространственным координатам.

Граничные условия третьего рода представляют собой уравнения баланса потоков, характеризующих обмен энергией объекта с окружающей внешней средой.

В некоторых случаях, например для гетерогенных (неоднородных по составу материала) тепловых объектов, могут быть и иные граничные условия.

Состояние объекта характеризуется изменением во времени фазовых координат, определяемых в различных его точках. Задача анализа процесса функционирования технического объекта на микроуровне заключается в определении функций фазовых координат для множества точек, выделенных в области определения объекта.

Объекты с распределенными параметрами могут быть различной физической природы: механические, гидравлические, тепловые, электрические, магнитные и др.

Механические объекты представляют собой элементы и базовые детали машин и механизмов: корпуса, рамы, панели, валы, крылья самолетов, лопасти турбин и др. При анализе механических объектов находят деформации и напряжения. Они определяют несущую способность конструктивных элементов, надежность и нормальные условия функционирования базирующихся на них других элементов объекта.

При проектировании многих технических объектов возникает необходимость анализа теплонапряженности деталей, выбора оптимальных размеров и конфигурации теплообменников и решения многих других задач теплопередачи. В тепловых объектах определению подлежат температурные поля и термические напряжения.

При анализе гидравлических и пневматических систем определяют режимы течения сплошных потоков жидкостей и газов, характеризуемые скоростями и давлениями.

Обычно в исходные уравнения (2.1) входят не все фазовые координаты, характеризующие процессы функционирования технического объекта, а только базисные, например деформации — в модели механической системы, температуры — в тепловой системе и т.д. Остальные фазовые координаты (например, напряжения в упомянутых системах) определяют через базисные координаты на основе уравнений, устанавливающих между ними соответствующие соотношения.