
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Данные о количестве браков в России в 1996-1997 гг., тыс.
|
|
| Год | I кв. | II кв. | III кв. | IV кв. |
| 183,1 | 187,9 | 294,1 | 201,6 | |
| 197,3 | 177,4 | 286,5 | 184,6 |
Решение. Определим, имеет ли данный ряд динамики общую тенденцию развития. Для этого рассчитаем средний темп роста по формуле (4.10).
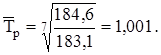
Так как средний темп роста близок к 1, делаем вывод об отсутствии общего тренда. В этом случае расчет среднего индекса сезонности произведем по способу постоянной средней.
Вначале рассчитаем средние уровни одноименных внутригодовых периодов по формуле (4.32):
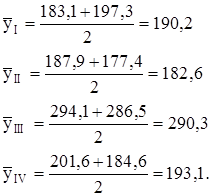
По формуле (4.33) определим общий средний уровень ряда за 2 года:
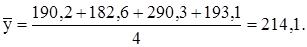
Средние индексы сезонности рассчитаем по формуле (4.31) отдельно для каждого квартала:
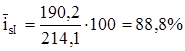
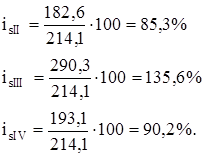
Таким образом, можно сделать вывод о том, что пик браков в России приходится на III квартал, уровень которого на 35,6% превышает среднеквартальное количество браков.
Задача 4.4
По приведенному ряду динамики рассчитайте уровень явления в 1989 г. и спрогнозируйте уровень 2001 г., используя метод экстраполяции:
Таблица 4.6
| Показатели | ||||||||
| Число вагонов на конец года, тыс. шт. | - | 4,3 | 4,57 | 5,37 | 5,70 | 5,96 | 6,21 | 6,41 |
Решение. При использовании метода экстраполяции предварительно выбирают одну из двух формул: (4.34) или (4.35). чтобы выбрать формулу, следует определить характер динамики: равномерное или равноускоренное развитие имеет показатель.
Для этого рассчитывают абсолютные приросты и темпы роста по формулам (4.1) и (4.2) соответственно. При равномерном темпе для экстраполяции используют формулу (4.34), при равноускоренном - (4.35).
В данном примере начинать с расчета показателей динамики нецелесообразно, т.к. данные приводятся не за каждый год. Поэтому расчет недостающего показателя - уровня 1989 - сделаем двумя способами.
I способ. Используем для расчета формулу (4.34). для этого предварительно рассчитаем средний за период абсолютный прирост (4.8):
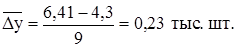
Числитель равен 9, т.к. данные приведены за 10 лет, с 1990 по 1999 гг.
Тогда уровень 1989 г. будет равен:
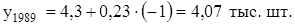
В данном случае l = -1, т.к. мы определяем уровень предыдущего года, т.е. экстраполируем на 1 год назад.
II способ. Используем для расчета уровня 1989 г. формулу (4.27). Расчет среднего темпа роста по формуле (4.10):
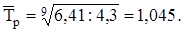
Тогда уровень 1989 г. будет равен:
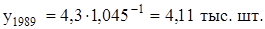
Как видно из расчетов, использование разных формул дает неодинаковые результаты, но расхождение незначительное, всего 0,04 тыс. штук, поэтому пользоваться можно любым полученным значением уровня 1989 г.
Для расчета уровня явления 2001 г. исходим из того, что прогноз необходимо произвести на 2 года вперед, начиная со значения признака в 1999 г. Тогда, используя I способ, найдем возможное количество вагонов в 2001 г.:

Второй способ дает следующее значение признака:
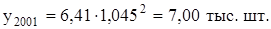
Задача 4.5
По данным об инвестициях в основной капитал произвести аналитическое выравнивание ряда динамики на основе функции прямой и параболы второго порядка. Выбрать уравнение, наиболее точно описывающее динамику показателя.
Таблица 4.7
Инвестиции в основной капитал в январе-сентябре 1998 г., млрд руб.*
| Дата | январь | февраль | март | апрель | май | июнь | июль | август | сентябрь |
| Инвестиции в основной капитал, млрд руб. | 22,1 | 23,7 | 26,1 | 25,5 | 26,6 | 31,8 | 32,9 | 35,4 | 38,8 |
Решение. Произведем выравнивание исходных данных по уравнению прямой. Для расчета параметров уравнения прямой и выровненных значений уровней ряда построим табл. 4.8.
Таблица 4.8
| yi | ti | tiyi | 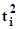
| 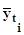
| 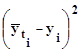
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 22,1 | 22,1 | 19,06+2,03·1=21,09 | (21,09-22,1)2=1,020 | ||
| 23,7 | 47,4 | 19,06+2,03·2=23,12 | (23,12-23,7)2=0,336 | ||
| 26,1 | 78,3 | 19,06+2,03·3=25,15 | (25,15-26,1)2=0,902 | ||
| 25,5 | 102,0 | 27,18 | 2,822 | ||
| 26,6 | 133,0 | 29,21 | 6,812 | ||
| 31,8 | 190,8 | 31,24 | 0,314 | ||
| 32,9 | 230,3 | 33,27 | 0,137 | ||
| 35,4 | 283,2 | 35,30 | 0,01 | ||
| 38,8 | 349,2 | 37,33 | 2,161 | ||
| Σ=262,9 | Σ=45 | Σ=1436,3 | Σ=285 | Σ=262,89 | Σ=14,514 |
Расчеты параметров ао и а1 произведем по формулам (4.12) и (4.14):

Следовательно, уравнение прямой имеет вид:
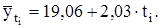
Подставляя значения ti из табл. 4.8 (гр. 2) в уравнение прямой, рассчитаем теоретические (выровненные) значения уровней ряда, которые записываем в гр. 5 табл. 4.8. Правильность расчетов теоретических значений 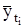 проверяется при помощи следующего равенства:
проверяется при помощи следующего равенства:
 .
.
В нашем примере  Следовательно, расчеты сделаны правильно.
Следовательно, расчеты сделаны правильно.
В графе 6 табл. 4.8 определяются квадраты отклонения выровненных значений  от реальных значений уi, на основе которых находят стандартизированную ошибку аппроксимации для уравнения прямой (формула (4.28).
от реальных значений уi, на основе которых находят стандартизированную ошибку аппроксимации для уравнения прямой (формула (4.28).
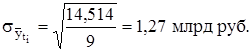
Для выравнивания ряда по уравнению параболы второго порядка воспользуемся более простым способом расчетов - от условного нуля. Для проведения расчетов составляем табл. 4.9.
Таблица 4.9
| yi | ti | 
| 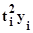
| 
| 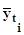
| 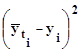
| tiyi |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 22,1 | -4 | 353,6 | 28,2+2,03(-4)+ +0,15·16=22,5 | (22,5-22,1)2=0,16 | -88,4 | ||
| 23,7 | -3 | 213,3 | 28,2+2,03(-3)+ +0,15·9=23,4 | (23,4-23,7)2=0,009 | -71,1 | ||
| 26,1 | -2 | 104,4 | 28,2+2,03(-2)+ +0,15·4=24,7 | (24,7-26,1)2=1,96 | -52,2 | ||
| 25,5 | -1 | 25,5 | 26,3 | 0,64 | -25,5 | ||
| 26,6 | 28,2 | 2,56 | |||||
| 31,8 | 31,8 | 30,4 | 1,96 | 31,8 | |||
| 32,9 | 131,6 | 32,8 | 0,01 | 65,8 | |||
| 35,4 | 318,6 | 35,6 | 0,04 | 106,2 | |||
| 38,8 | 620,8 | 38,7 | 0,01 | 155,2 | |||
| Σ=262,9 | Σ=0 | Σ=60 | Σ=1799,6 | Σ=708 | Σ=262,6 | Σ=7,43 | Σ=121,8 |
Рассчитаем параметры уравнения ао, а1, а2 по формулам (4.16), (4.17), (4.18).
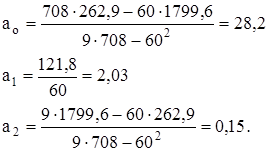
Уравнение параболы второго порядка в данном примере:

Подставляя значения ti в данное уравнение, рассчитаем теоретические уровни 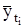 (гр. 6 табл. 4.9). Сравнивая суммарные теоретические и реальные уровни ряда (итог гр. 1 и итог гр. 6 табл. 4.9), судим о правильности расчетов теоретических уровней.
(гр. 6 табл. 4.9). Сравнивая суммарные теоретические и реальные уровни ряда (итог гр. 1 и итог гр. 6 табл. 4.9), судим о правильности расчетов теоретических уровней.
Для расчета стандартизованной ошибки аппроксимации суммируем возведенные в квадрат отклонения теоретических и реальных уровней (гр. 7 табл. 4.9). ошибка аппроксимации равна:

Чтобы выбрать наиболее подходящее уравнение, сравним стандартизованные ошибки аппроксимации для уравнения прямой и уравнения параболы. В первом случае ошибка равна 1,27 млрд руб., во втором - 0,91 млрд руб. таким образом, наиболее точно анализируемый ряд динамики описывается уравнением параболы второго порядка.
* Вопросы статистики. - 1999. - № 2, с. 84.
* Вопросы статистики. - 1999. - № 2, с. 77.
* Вопросы статистики. - 1999. - № 2, с.80.
Date: 2016-07-18; view: 465; Нарушение авторских прав