Определение параметров уравнения регрессии.

Существует два вида корреляции: парная и множественная.

Парная рассматривает влияние вариации факторного признака «х» на результативный признак «у».

Множественная корреляция рассматривает влияние нескольких факторных признаков «х1», «х2» и т.д. на результативный признак «у».

При изучении связей показателей экономической деятельности применяются различные уравнения, называемые уравнениями регрессии. Они выражают изменение среднего уровня признака «у» в зависимости от изменения среднего уровня признака «х».

Уравнения регрессии устанавливают характер связи между признаками и могут быть линейными и криволинейными.

Линейная форма связи предполагает равномерное изменение результативного признака «у» под воздействием факторного признака «х». Уравнение регрессии имеет вид:

(4.1)

Не все связи можно выразить линейным уравнением регрессии, часто применяются следующие уравнения:

- параболы второго порядка:

, (4.2)

- параболы третьего порядка:

, (4.3)

- показательной функции:

, (4.4)

- полулогарифмической функции:

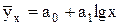, (4.5)

где - теоретические значения результативного признака;

а₀, а₁, а₂, а₃ - параметры уравнения регрессии;

х - эмпирические (реальные) значения факторного признака.

и т.д.

Поэтому, первый этап корреляционного анализа – выбор формы уравнения связи.

Второй этап корреляционного анализа – определение параметров уравнения.

Для определения параметров уравнения регрессии применяется метод наименьших квадратов:

(5)

Базируясь на методе наименьших квадратов, можно составить следующие системы нормальных уравнений для расчета параметров а₀, а₁ и т.д.:

а) для уравнения прямой

(6.1)

б) для уравнения параболы второго порядка

(6.2)

в) для показательной функции

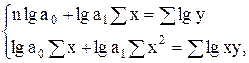(6.3)

г) для полулогарифмической функции

(6.3)

Для определения параметров уравнений может использоваться либо способ совместного решения уравнений, либо способ определителей.

По способу определителей параметры уравнения прямой находятся следующим образом:

(7.1)

Параметры уравнения показательной функции:

(7.2)

Параметры уравнения полулогарифмической функции по методу определителей равны:

(7.3)

Смысл параметров уравнения:

А₀ показывает значение признака у_х, не зависящее от значений «х».

А₁ называется коэффициентом регрессии и показывает, на сколько единиц в среднем изменится значение «у» при изменение «х» на единицу. А₁ может иметь знак (+) или (-). При наличии знака минус между признаками «х» и «у» имеется обратная линейная связь.

Date: 2016-07-18; view: 326; Нарушение авторских прав