Определение ошибки выборки.

Выборочное наблюдение основано на принципе равной возможности попадания единиц генеральной совокупности в выборочную. Это позволяет избежать систематических ошибок наблюдения. Однако, в связи с тем, что исследуемая совокупность состоит из единиц с варьирующими признаками, состав выборки может отличаться от состава генеральной совокупности, вызывая расхождения между генеральными и выборочными характеристиками.

Такие расхождения называются ошибками репрезентативности или ошибками выборки.

Определение ошибки выборки – основная задача, решаемая при выборочном наблюдении.

В математической статистике доказывается, что средняя ошибка выборки определяется по формуле:

(1)

Где m - ошибка выборки;

s²₀ – дисперсия генеральной совокупности;

n – количество единиц выборочной совокупности.

На практике для определения средней ошибки выборки используется дисперсия выборочной совокупности s².

Между генеральной и выборочной дисперсиями существует равенство:

(2).

Из формулы (2) видно, что генеральная дисперсия больше выборочной на величину (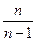). Однако при достаточно большой величине выборки это соотношение близко к единице, поэтому можно записать, что

(3)

Однако такая формула для определения средней ошибки выборки применяется только при повторном отборе.

На практике обычно применяется бесповторный отбор и средняя ошибка выборки рассчитывается несколько иначе, так как численность выборки в ходе исследования сокращается:

(4)

где n – численность выборочной совокупности;

N – численность генеральной совокупности;

s² - выборочная дисперсия.

Для доли альтернативного признака средняя ошибка выборки при бесповторном отборе определяется по формуле:

(5), где

w (1-w) - средняя ошибка выборочной доли альтернативного признака;

w – доля альтернативного признака выборочной совокупности.

При повторном отборе средняя ошибка доли альтернативного признака определяется по упрощенной формуле:

(6)

Если численность выборки не превышает 5%, средняя ошибка выборочной доли и выборочной средней определяется по упрощенным формулам (3) и (6).

Определение средней ошибки выборочной средней и выборочной доли необходимо для установления возможных значений генеральной средней (х) и генеральной доли (Р) на основе выборочной средней (х) и выборочной доли (w).

Одно из возможных значений, в пределах которого находится генеральная средняя, определяется по формуле:

(7)

Для генеральной доли этот интервал можно записать в виде:

(8)

Полученные таким образом характеристики доли и средней в генеральной совокупности отличаются от величины выборочной доли и выборочной средней на величину m. Однако гарантировать это можно не с полной уверенностью, а лишь с определенной степенью вероятности.

В математической статистике доказывается, что пределы значений характеристик генеральной и выборочной средней отличаются на величину m лишь с вероятностью 0,683. Следовательно, только в 683 случаях из 1000 генеральная средняя находится в пределах х= х m_х, в остальных случаях она выйдет за эти пределы.

Вероятность суждений можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную в t раз.

Множитель t называют коэффициентом доверия. Он определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты исследования.

Математик А.М.Ляпушев рассчитал различные значения t, которые обычно приводятся в готовых таблицах.

При использовании коэффициента доверия формула для определения интервалов выборочной средней примет следующий вид:

(9)

где выражение t m_х - предельная ошибка выборки. Обозначается D_х.

Генеральная доля в этом случае будет рассчитана аналогично:

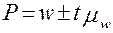(10)

Таким образом, из формул (4) и (9), предельная ошибка выборочной средней в общем виде записывается:

(11)

Предельная ошибка выборочной доли соответственно примет вид:

(12)

Эти формулы применяются при бесповторном отборе. При повторном отборе или при малой численности выборки (до 5%), предельная ошибка выборочной средней примет вид:

(13)

Предельная ошибка выборочной доли при малой численности выборки (до 5%) или при повторном отборе:

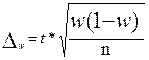(14)

Date: 2016-07-18; view: 261; Нарушение авторских прав