Нули функции. Асимптота.

Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f (x)определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимаетфункция, называется областью значений функции. Теперь можно дать болееточное определение функции: правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества Xможно найти один и только один элемент из множества Y, называетсяфункцией.

Из этого определения следует, что функция считается заданной, если:

- задана область определения функции X;

- задана область значений функции Y;

- известно правило (закон) соответствия, причём такое, что для каждого

значения аргумента может быть найдено только одно значение функции.

Это требование однозначности функции является обязательным.

Монотонная функция. Если для любых двух значений аргумента x ₁ и x ₂ из условия x ₂> x ₁ следует f (x ₂) > f (x ₁ ), то функция f (x)называется возрастающей; если для любых x ₁ и x ₂ из условия x ₂> x ₁ следует f (x ₂) < f (x ₁), то функция f (x) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.

Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что | f (x) | M для всех значений x. Если такого числа не существует, то функция - неограниченная.

П р и м е р ы.

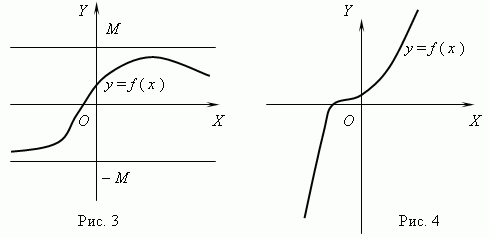
Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная. (Объясните это, пожалуйста!).

Непрерывная и разрывная функции. Функция y = f (x) называется непрерывной в точке x = a, если:

1) функция определена при x = a, т.e. f (a) существует;

2) существует конечный предел lim f (x);

x → a

(см. раздел «Пределы функций» в главе «Основы анализа»)

3) f (a) = lim f (x).

x → a

Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a.

Если функция непрерывна во всех точках своей области определения, тоона называется непрерывной функцией.

Чётная и нечётная функции. Если для любого x из области определенияфункции имеет место: f (- x) = f (x), то функция называется чётной; если же имеет место: f (- x) = - f (x), то функция называется нечётной. График чётной функции симетричен относительно оси Y (рис.5), a график нечётной функции симметричен относительно начала координат (рис.6).

Периодическая функция. Функция f (x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f (x + T) = f (x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

П р и м е р 1. Доказать, что sin x имеет период 2 .

Р е ш е н и е. Мы знаем, что sin (x+ 2 n) = sin x, где n = 0, ± 1, ± 2, …

Следовательно, добавление 2 n к аргументу синуса не

меняет его значениe. Существует ли другое число с таким

же свойством?

Предположим, что P – такое число, т.e. равенство:

sin (x+ P) = sin x,

справедливо для любого значения x. Но тогда оно имеет

место и при x = / 2, т.e.

sin ( / 2 + P) = sin / 2 = 1.

Но по формуле приведения sin ( / 2 + P) = cos P. Тогда

из двух последних равенств следует, что cos P = 1, но мы

знаем, что это верно лишь при P = 2 n. Так как наименьшим

отличным от нуля числом из 2 n является 2 , то это число

и есть период sin x. Аналогично доказывается, что 2

является периодом и для cos x.

Докажите, что функции tan x и cot x имеют период .

П р и м е р 2. Какое число является периодом функции sin 2 x?

Р е ш е н и е. Рассмотрим sin 2 x = sin (2 x + 2 n) = sin [ 2 (x + n) ].

Мы видим, что добавление n к аргументу x, не меняет

значение функции. Наименьшее отличное от нуля число

из n есть , таким образом, это период sin 2 x.

Нули функции. Значение аргумента, при котором функция равна 0, называется нулём (корнем) функции. Функция может иметь несколько нулей.Например, функция y = x (x + 1) (x -3) имеет три нуля: x = 0, x = -1, x = 3. Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х.

На рис.7 представлен график функции с нулями: x = a, x = b и x = c.

Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой.

Обратная функция

Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:

v = u ²,

где u - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v:

Если обозначить аргумент в обеих функциях через x, а функцию – через y, то мы имеем две функции:

каждая из которых является обратной по отношению к другой.

П р и м е р ы. Эти функции являются обратными друг к другу:

1) sin x и Arcsin x, так как, если y = sin x, то x = Arcsin y;

2) cos x и Arccos x, так как, если y = cos x, то x = Arccos y;

3) tan x и Arctan x, так как, если y = tan x, то x = Arctan y;

4) e^x и ln x, так как, если y = e^x, то x = ln y.

Сложная функция

Рассмотрим функцию:

y = sin ² (2 x).

Фактически эта запись означает следующую цепочку функциональных преобразований:

u = 2 x --> v = sin u --> y = v ²,

что может быть записано в общем виде с помощью символов функциональных зависимостей:

u = f ₁(x) --> v = f ₂ (u) --> y = f ₃(v),

или короче:

y = f { v [ u (x) ] }.

Мы имеем здесь не одно правило соответствия для преобразования x в y, а три последовательных правила соответствия (т.е. функции), используя которые мы получаем y как функцию от x. В этом случае мы говорим, что y – сложная функция от x.