Понятие простого и сложного процента

Стандартным временным интервалом в финансовых операциях является 1 год, поэтому распространен вариант, когда процентная ставка устанавливается в виде годовой ставки. Годовая ставка подразумевает однократное начисление процентов по истечении года после получения ссуды. Существует две основные схемы дискретного начисления:

· Схема простых процентов;

· Схема сложных процентов.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Таким образом, размер инвестиционного капитала (R_n) через n лет будет равен:

(5)

где:

R_n – величина накопления;

Р – первоначальный вклад;

r – процентная ставка (в долях единицы);

n – число периодов начисления процентов.

Простой процент начисляется только один раз в конце срока депозитного договора.

Сложный процент, представляет геометрическую зависимость (рис. 8) между первоначальным вкладом, процентной ставкой и периодом накопления.

Инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные проценты.

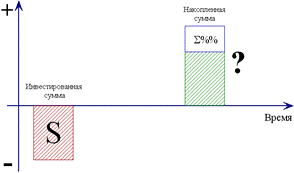
Рис. 8. Рост основной суммы по сложному проценту.

В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время увеличивается.

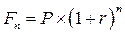(6)

Формула сложных процентов является одной из базовых формул, поэтому для удобства пользования значения множителя FM1(r,n), называемого мультиплицирующим множителем для единичного платежа, рассчитаны для различных значений r и n.

Формула алгоритма наращения по схеме сложных процентов переписывается следующим образом:

где: (7)

Экономический смысл множителя FM1(r,n) состоит в следующем: он показывает, чему будет равна одна денежная единица через n периодов при заданной процентной ставке.

Таким образом, сложный процент предполагает начисление процентов не только на сумму первоначального взноса, но и на сумму процентов, накопленных к концу каждого периода. Это возможно только в случае реинвестирования суммы начисленных процентов, т.е. присоединения их к инвестированному капиталу.

Очень важно знать при проведении финансовых операций, как соотносятся величины R_n и F_n (рис. 9).

Рис. 9. Графическая взаимосвязь между простой и сложной схемой наращения капитала.

Таким образом:

1. Более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода).

R_n>F_n при 0<n<1

2. Более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно).

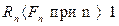
3. Обе схемы дают одинаковые результаты при продолжительности периода один год и однократном начислении процентов.

При сроках погашения до одного года в качестве показателя n берется величина, характеризующая удельный вес длины подпериода (день, месяц, квартал, полугодие) в общем периоде (год). Длина различных временных интервалов в расчетах может округляться: месяц – 30 дней; квартал – 90 дней; полугодие – 180 дней; год – 360 (365, 366) дней.

Периодичность начисления процентов оказывает влияние на величину накопления. Чем чаще начисляются проценты, тем больше накопленная сумма. При более частом накоплении необходимо откорректировать процентную ставку и число периодов начисления процентов:

(8)

(9)

При пользовании финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки, т.е. если базисным периодом начисления процентов является квартал, то в расчетах должна использоваться квартальная ставка.

Достаточно обыденным являются контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним из двух методов:

– по схеме сложных процентов:

(10)

где: w – целое число периодов;

f – дробное число периодов.

– по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов для дробной части года):

(11)

При использовании смешанной схемы наращенная сумма будет больше.

Возможно начисление процентов по внутригодовым подпериодам, а продолжительность общего периода действия не равна целому числу подпериодов. В этом случае также возможно использование двух схем:

– по схеме сложных процентов:

(12)

где: m – количество начислений в году.

– по смешанной схеме:

(13)

В алгоритмах показатели w и f имеют разный смысл. В формуле (11) w означает целое число лет в n годах, а f – дробную часть года, и поэтому n = w + f. В формуле (13) w означает целое число подпериодов в n годах, а f – дробную часть подпериода, поэтому n = (w + f)/m.

Date: 2016-11-17; view: 549; Нарушение авторских прав