Законы геометрической оптики

При решении многих задач оптики можно отвлечься от волновой природы света. Если размеры отверстий и препятствий велики в сравнении с длиной световой волны, то дифракционными явлениями можно пренебречь и считать распространение света прямолинейным. При этом описание явлений и анализ действия различных устройств сводится к рассмотрению геометрии хода световых лучей.

Геометрическую оптику можно считать предельным случаем волновой оптики, когда длина волны очень мала в сравнении с другими размерами, учитываемыми в решаемой задаче.

В основе геометрической оптики лежит принцип, сформулированный в 1660 г. П.Ферма. В простейшей формулировке этот принцип звучит так: в пространстве между двумя точками свет распространяется по тому пути, вдоль которого время его прохождения минимально.

Величина, равная отношению скорости света с в вакууме к скорости υ в данной среде, называется абсолютным показателем преломления этой среды:

.

В вакууме скорость света максимальна. В оптической среде с показателем преломления n время прохождения светом того же расстояния увеличивается в n раз. Величина s, равная произведению абсолютного показателя преломления n на пройденное расстояние l (s= nl), называется оптической длиной пути.

Используя принцип Ферма, можно получить законы прямолинейного распространения света, отражения и преломления.

Прямолинейность распространения света. Свет из одной точки в другую распространяется по кратчайшему расстоянию. В однородной среде кратчайшим оптическим путем является прямая линия.

Однако в неоднородной среде кратчайшим оптическим путем может оказаться некоторая кривая (или ломаная) линия, вдоль которой показатель преломления меньше, чем вдоль геометрической прямой. Этим объясняется явление преломления света и искривление световых лучей в неоднородной среде – явление рефракции.

Закон отражения. Пусть на зеркальную поверхность падает свет из точки А. В точке А* собираются лучи, отраженные от зеркала (рис. 92). Предположим, что свет из точки А в точку А* может распространяться двумя путями – отражаясь от точек О и О*. Время, которое потребуется свету, чтобы пройти из источника А в точку А* через точку О, можно определить из выражения

.

Здесь υ – скорость распространения света. Покажем, что время прохождения света по траектории АО А* меньше, чем по любой другой траектории АО* А*.

Для этого продифференцируем данное выражение и приравняем производную к нулю в соответствии с принципом Ферма. Учтем, что , . Получим:

.

Отсюда получаем 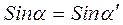; а так как оба угла острые, то отсюда следует равенство углов:

.

Мы получили соотношение, выражающее закон отражения света: угол отражения равен углу падения. Из принципа Ферма следует и вторая часть этого закона: отраженный луч лежит в плоскости, проходящей через падающий луч и нормаль к отражающей поверхности. Ведь если бы эти лучи лежали в разных плоскостях, то не был бы минимальным путь АО А*.

Закон преломления света. Аналогичным образом, используя принцип Ферма, рассмотрим явление, происходящее на границе раздела двух сред. Пусть в первой среде скорость света υ₁, а во второй среде – υ₂ (рис. 93). Для прохождения света из точки А₁ в точку А₂ будет затрачено время

.

Выберем из всех возможных траекторий распространения света ту, которой соответствует минимальное время. Продифференцировав и положив производную равной нулю, получим:

.

Учитывая, что , , получим:

.

Откуда следует:

.

Это и есть закон преломления света. Из построений и принципа Ферма следует также, что преломленный луч лежит в плоскости, проходящей через падающий луч и перпендикуляр к поверхности раздела двух сред.

Из закона преломления света вытекает, что при падении света из оптически менее плотной среды в более плотную (n₁<n₂) угол падения больше угла преломления (α₁>α₂). Если же свет идет из оптически более плотной среды в менее плотную (n₁>n₂), то угол падения меньше угла преломления (α₁<α₂) (рис. 94). В этом случае при некотором угле падения α₁, большем предельного, пучок света, падающий на границу раздела, отражается от нее как от зеркала. Это явление получило название полного отражения. Найдем значение предельного угла:

;

.

Явлением полного отражения объясняется исключительная белизна свежевыпавшего снега (он отражает более 90% падающих на него солнечных лучей). Предположим, что световые лучи падают на границу льда и воздуха изнутри льда. В этом случае все лучи с углами падения больше 48⁰ будут полностью отражаться от границы лед – воздух. Снег – это, в конечном счете, лед (ведь снежинки состоят из мелких льдинок), но лед этот не монолитен, а пронизан множеством воздушных пор. Попадая на поверхность снега, солнечные лучи сравнительно легко проникают внутрь снеговых льдинок, находящихся вблизи поверхности. Проникнуть глубже в снег лучам не дают полные отражения от многочисленных поверхностей, отделяющих льдинки от воздуха, который заполняет внутренние поры в снегу. Когда эти поры исчезают (при образовании монолитного льда или в результате заполнения талой водой), отражение света существенно уменьшается – в этом случае значительная часть солнечных лучей проникает достаточно глубоко внутрь покрова и там поглощается.

На явлении полного внутреннего отражения основано появление целого раздела оптики – волоконной оптики, в котором изучается формирование изображений при распространении света по световодам. Свет от источника распространяется по световодам, диаметр которых в зависимости от назначения колеблется от нескольких микрометров до миллиметров. В применяемом стеклянном волокне основная световедущая жила окружена оболочкой с меньшим показателем преломления (рис. 95). На границе раздела двух сред происходит полное отражение света. За счет этого световой пучок практически без потерь проходит от источника к освещаемой поверхности.

Применение различных устройств волоконной оптики очень широко: от техники до медицины. Например, одножильные световоды уже много лет применяют для освещения внутренних поверхностей желудка, мочевого пузыря и других внутренних органов при диагностике и проведении операций. В технике световоды применяются для освещения недоступных мест, а также для передачи сигналов на большие расстояния. Моделируя световой пучок, идущий по световоду, можно по нему на значительные расстояния передавать информацию – речь, музыку, изображения, информацию от ЭВМ и т.п.

Линзы

Линза – это прозрачное тело (чаще из стекла или пластмассы), ограниченное двумя сферическими поверхностями с радиусами кривизны R₁ и R₂. Одна из поверхностей линзы может быть плоской (R=¥). По форме ограничивающих поверхностей различают шесть типов линз: двояковыпуклая, плосковыпуклая, вогнуто-выпуклая, двояковогнутая, плосковогнутая, выпукло-вогнутая (рис. 96).

Тонкой называется линза, толщина которой значительно меньше радиусов ограничивающих ее сферических поверхностей. Линза, которая в середине толще, чем у краев, называется выпуклой (собирающей) линзой (рис. 96, а, б, в). Линза, которая у краев толще, чем в середине, называется вогнутой (рассеивающей) линзой (рис. 96, г, д, е).

Прямая, проходящая через центры О₁ и О₂ сферических поверхностей линзы, называется главной оптической осью линзы (рис. 97). Если толщина пренебрежимо мала, то можно считать, что главная оптическая ось пересекается с линзой в одной точке. Точка О пересечения главной оптической оси, с тонкой линзой называется оптическим центром линзы.

Опыт показывает, что луч света, идущий вдоль главной оптической оси, проходит через линзу без изменения направления распространения. В воздухе или в вакууме все лучи, параллельные главной оптической оси собирающей линзы, после прохождения линзы отклоняются к оси и проходят через одну точку F на главной оптической оси (рис. 98, а). Точка F называется главным фокусом линзы. Плоскость, проходящая через главный фокус линзы перпендикулярно главной оптической оси, называется фокальной плоскостью.

У линзы два главных фокуса в однородной среде расположены на одинаковых расстояниях от ее оптического центра. Расстояние оптического центра линзы до главного фокуса – фокусное расстояние линзы. Все лучи, проходящие через один из главных фокусов, выходят из линзы параллельно главной оптической оси.

В воздухе или вакууме все лучи, параллельные главной оптической оси рассеивающей линзы, отклоняются от оптической оси. Продолжения лучей в противоположную сторону сходятся в одной точке F на главной оптической оси перед линзой (рис. 98, б). Эта точка называется главным мнимым фокусом (в действительности лучи света в нем не собираются).

Основное свойство линз, используемое в оптических приборах, заключается в том, что все лучи, исходящие из одной точки А перед линзой, собираются в другой точке А₁ за линзой (рис. 99, а) или кажутся исходящими из одной точки А₂ перед линзой (рис. 99, б). В первом случае изображение точки А называется действительным, во втором – мнимым.

Замечательным свойством лучей является свойство обратимости: луч, направленный противоположно лучу, выходящему из любой оптической системы, пройдет через нее в обратном направлении точно по тому же пути, по какому прошел ее в прямом направлении первый луч.

Используя свойства лучей, проходящих через оптический центр линзы или ее фокусы, а также лучей, параллельных главной оптической оси можно построить изображение любого предмета, получаемое с помощью собирающей или рассеивающей линзы. Условные изображения собирающей и рассеивающей линз представлены на рисунке 100.

Расстояние f от собирающей линзы до изображения связано с расстоянием d от предмета до линзы и фокусным расстоянием F линзы:

.

Это уравнение называется формулой линзы. Данная формула применима для нахождения расстояния до изображения при любом расположении предмета относительно линзы.

Если значение расстояния f получается при расчете отрицательным, то это значит, что изображение предмета мнимое и находится по ту же сторону от линзы, что и предмет. Для рассеивающей линзы значение фокусного расстояния в расчетах нужно брать со знаком «минус» и, так как изображение предмета получаем мнимым, расстояние f до изображения всегда должно быть со знаком «минус».

Величина, обратная фокусному расстоянию F, называется оптической силой линзы D:

.

Оптическая сила выражается в диоптриях (дптр.). Оптическая сила собирающей линзы положительна, оптическая сила рассеивающей линзы отрицательна.

Date: 2016-11-17; view: 1228; Нарушение авторских прав