Сложение гармонических колебаний

Одна и та же материальная точка может участвовать одновременно в двух или более колебаниях. Нахождение закона результирующего колебательного движения называется сложением колебаний. Рассмотрим несколько простых случаев сложения гармонических колебаний.

1.Сложение двух гармонических колебаний одного направления с равными частотами w, одинаковыми амплитудами А и разностью фаз Dj:

;

.

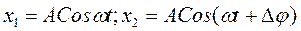Результирующее колебание является также гармоническим и имеет частоту w. Его амплитуда

зависит от разности фаз D j слагаемых колебаний. При D j=±2kp амплитуда максимальна (А_рез=2А) – складывающиеся колебания друг друга усиливают. При D j=±(2k+1)p колебания складываются «в противофазе» и взаимно друг друга гасят (А_рез=0). В случае когда амплитуды А₁ и А₂ слагаемых колебаний неодинаковы, А_рез=А₁+А₂ при D j=±2kp и А_рез= ç А₁-А₂ ç при D j=±(2k+1)p.

2. Сложение взаимно перпендикулярных колебаний. Если частоты слагаемых колебаний относятся как целые числа, то точка описывает сложные замкнутые кривые – фигуры Лиссажу, форма которых зависит от соотношения частот и разности фаз исходных колебаний. Фигуры Лиссажу можно наблюдать на экране осциллографа, заставив электронный луч колебаться во взаимно перпендикулярных направлениях. Если частоты двух колебаний одинаковы, а их фазы отличаются на p/2:

,

то результирующее движение точки происходит по плоской траектории, уравнение которой

.

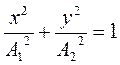Эта траектория – эллипс, оси которого совпадают с осями x и y (рис. 81). Форма и расположение эллипса могут меняться с изменением разности фаз исходных колебаний (рис. 82). Он, в частности, может выродиться в прямую.

Date: 2016-11-17; view: 699; Нарушение авторских прав