Гармонические колебания и их характеристики

Колебаниями называются процессы, характерной особенностью которых является повторяемость. Это могут быть качания маятников и сооружений, тепловые колебания ионов в кристаллической решетке, ритмичные сокращения сердца и т.п. Колебания любой природы подчиняются общим законам. Особое значение имеют периодические колебания, в процессе которых система возвращается в исходное состояние через равные промежутки времени Т. Длительность этих промежутков времен называется периодом колебания. Величина

,

показывающая, сколько раз в секунду повторяется колебание, называется частотой и измеряется в герцах:

.

Перечислим примеры периодических процессов в биологии: многие цветы закрывают венчики с наступлением темноты; у большинства животных наблюдается годовая периодичность появления потомства; известно периодическое изменение интенсивности фотосинтеза у растений, колебания испытывают размеры ядер в клетках, численность животных определенного вида, проживающих в данном районе, и т.д.

Простейшими колебаниями являются гармонические, происходящие по закону косинуса (или синуса):

,

где x – величина, периодически меняющаяся во времени, А – модуль ее максимального значения (амплитуда), t – время, – циклическая частота.

Величина

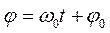
называется фазой колебания, а j₀ – начальной фазой колебания. За время, равное периоду, фаза колебания изменяется на 2p.

Физическая система, совершающая колебания около положения равновесия, называется осциллятором. Простейший гармонический осциллятор – материальная точка, совершающая гармонические колебания вдоль прямой.

Гармонические колебания совершает, например, груз, подвешенный на невесомой пружине (рис. 77). Его движение можно свести к движению материальной точки – центра масс груза. В этом случае x – смещение точки от положения равновесия. Скорость и ускорение гармонического осциллятора можно найти, взяв первую, а затем вторую производную от x по времени:

,

.

Здесь – амплитуда скорости точки и – амплитуда ускорения. Величины x, υ, а изменяются гармонически во времени с одинаковой частотой, но сдвинуты друг относительно друга по фазе: скорость опережает смещение на p/2, а ускорение опережает смещение на p (рис. 78).

Сопоставив выражения для x и a, заметим, что

.

Отсюда можно получить выражение для силы, вызывающей и поддерживающей гармонические колебания:

,

где . Эта сила пропорциональна смещению и всегда направлена к положению равновесия. Такой силой является, в частности, сила упругости. Силы, неупругие по природе, но удовлетворяющие условию F=-kx, называются квазиупругими. Тело может совершать гармонические колебания, если на него действует упругая или квазиупругая сила.

Колебания системы, выведенной из положения равновесия и далее предоставленной самой себе, называются свободными. Подставив во второй закон Ньютона выражение для квазиупругой силы, получим:

,

или

.

Это уравнение свободных колебаний гармонического осциллятора. Здесь

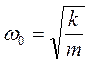
есть собственная частота колебательной системы. Период свободных колебаний выражается следующим образом:

.

Замечательной особенностью гармонических свободных колебаний является независимость их частоты от амплитуды. Частота определяется только свойствами самой системы.

При гармонических колебаниях материальной точки происходят периодически взаимные превращения кинетической и потенциальной энергии. Величина полной энергии гармонического осциллятора массой m в любой момент времени равна сумме этих энергий:

,

или

.

Учитывая, что и подставив выражения для x и υ, получим:

.

В случае свободных колебаний полная энергия остается постоянной.

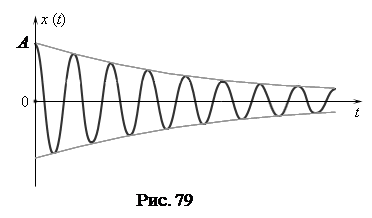
В реальных системах, однако, всегда имеются силы сопротивления, приводящие к рассеянию энергии. Колебания затухают (рис. 79).

Date: 2016-11-17; view: 677; Нарушение авторских прав