Последовательное и параллельное соединения проводников в электрической цепи

При последовательном соединении проводников (рис. 45, а) сила тока во всех проводниках одинакова – в противном случае заряды накапливались бы в каких-то точках цепи. Следовательно,

.

Измерив напряжение U на всей цепи, а затем на каждом из ее участков, можно установить, что

.

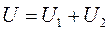Этот результат также следует из равенства работы по перемещению заряда по всей цепи сумме работ на участках.

Применяя закон Ома для участка цепи ко всей внешней цепи, сопротивление которой R, и к каждому из последовательно соединенных проводников, получаем:

.

Отсюда с учетом соотношения для напряжений следует:

,

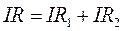или

.

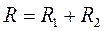При последовательном соединении полное сопротивление цепи равно сумме сопротивлений всех отдельных проводников.

Если цепь состоит не из двух, а из нескольких последовательно соединенных проводников с сопротивлениями R₁, R₂, R₃, … R_n, то общее сопротивление цепи

.

При параллельном соединении проводников (рис. 45, б) напряжения U₁ и U₂ одинаковы, так как резисторы присоединены к одним и тем же точкам цепи и равны напряжению на всей цепи:

.

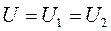Измерив силу тока в неразветвленной цепи и в каждой ее ветви, получаем:

.

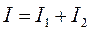Этот результат можно получить также из следующих соображений. Окружим мысленно точку А замкнутой поверхностью. За время t в эту поверхность за счет тока I втекает заряд q, а за счет токов I₁ и I₂ вытекают заряды q₁ и q₂. По закону сохранения электрического заряда

.

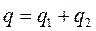Взяв производную по времени от обеих частей, получим соотношение для силы тока.

Из закона Ома для участка цепи следует:

.

Отсюда с учетом соотношения для силы тока получаем:

.

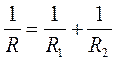Величина, обратная сопротивлению всего разветвленного участка цепи, равна сумме величин, обратных сопротивлениям каждого из параллельно соединенных проводников.

Все формулы, полученные для параллельного соединения двух проводников, справедливы для параллельного соединения любого их числа.

Шунт к амперметру. Дополнительное сопротивление к вольтметру. Каждый измерительный прибор рассчитывают на определенную максимальную для него силу тока или на предельное для него напряжение. Но всегда оказывается возможным расширить пределы измерения данным прибором.

Для увеличения предела измерения силы тока параллельно амперметру присоединяют проводник, через который проходит часть измеряемого тока. Сопротивление этого проводника, называемого шунтом, рассчитывают так, чтобы сила тока через амперметр не превышала его предельного значения, а остальная часть тока шла бы через шунт. При этом, разумеется, изменится цена деления шкалы данного прибора.

Поясним это примером. Амперметром, сопротивление которого равно R_a, рассчитанным на максимальную силу тока I_a, требуется измерить силу тока в цепи I_ц, которая может достигать значений, в n раз превышающих максимально допустимую силу тока в амперметре (I_ц=nI_a). Чему должно быть равно сопротивление R_ш шунта (рис. 46, а)?

Применяя формулы для параллельного соединения проводников, получаем:

и

.

Решая эти уравнения, найдем сопротивление шунта:

.

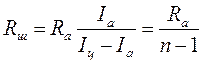Отсюда следует, что если амперметром, рассчитанным на силу тока, например, до 1 А, нужно измерить токи, в 10 раз большие (n=10), то сопротивление шунта должно быть меньше сопротивления амперметра в 9 раз. При этом цена каждого деления увеличивается в 10 раз, а точность измерения во столько же раз уменьшается.

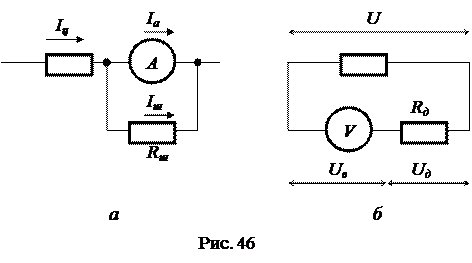
Чтобы увеличить пределы измерения напряжения вольтметром, последовательно ему подключают дополнительный резистор.

Определим, каким должно быть сопротивление резистора R_д (рис. 46, б), чтобы вольтметром, рассчитанным на максимальное напряжение U_в, можно было измерять напряжение U на резисторе R, в n раз большее (U=nU_в).

Применяя формулы для последовательного соединения проводников, получаем:

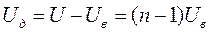
и

.

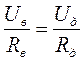Решая эти уравнения, найдем дополнительное сопротивление:

.

Обычно в технических приборах шунты к амперметрам и дополнительные сопротивления к вольтметрам находятся внутри самих приборов.

Правила Кирхгофа

Для упрощения расчета разветвленных цепей содержащих неоднородные участки Г.Р.Кирхгофом были созданы специальные правила.

Рассмотрим цепь, в некоторых точках которой (1 и 3) соединяются три проводника (рис. 47). Точки разветвленной цепи, в которых сходятся не менее трех проводников, называются узлами цепи.

В узлах не может происходить накопление зарядов или разрыв потока упорядоченно движущихся частиц. Поэтому суммарный ток, втекающий в узел, равен суммарному току, вытекающему из узла (рис. 48).

Если ток втекает в узел, то силу тока считают положительной величиной, если вытекает из узла, то отрицательной.

Первое правило Кирхгофа относится к узлам и формулируется следующим образом: алгебраическая сумма сил токов для каждого узла равна нулю:

.

В рассматриваемом случае (рис. 48) I₁ и I₂ – величины положительные, а I₃, I₄ и I₅ – отрицательные.

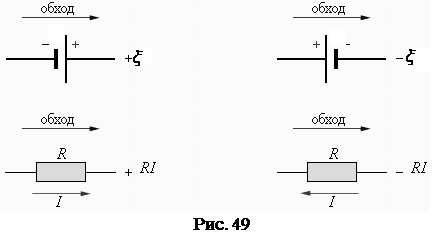
Второе правило Кирхгофа относится к замкнутым контурам разветвленной цепи. Условимся считать положительным направление обхода контура по часовой стрелке. Токи, идущие в положительном направлении обхода, будем считать положительными, противоположные токи – отрицательными. Точно также будем приписывать электродвижущим силам знак плюс, если они создают ток в положительном направлении обхода контура; в противном случае – знак минус (рис. 49). Второе правило Кирхгофа утверждает, что в замкнутом контуре разветвленной цепи алгебраическая сумма электродвижущих сил источников тока равна алгебраической сумме произведений сил тока на сопротивления соответствующих участков этого контура:

.

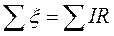При расчете разветвленной цепи надо, пользуясь правилами Кирхгофа, составить независимые уравнения для нескольких узлов и контуров; число уравнений должно равняться числу искомых величин (сил тока, э.д.с. и сопротивлений). Для составления независимых уравнений нужно использовать только такие контуры, которые различаются хотя бы одним участком, и только такие узлы, которые различаются хотя бы одной силой тока. Направления искомых сил тока выбираются произвольным образом. Если направление, принятое для какой-либо из сил тока, не соответствует действительному, то в результате расчета по правилам Кирхгофа эта сила получится отрицательной.

Рассмотрим замкнутый контур 1231; для него второе правило Кирхгофа запишется так:

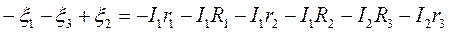
или

.

Аналогично для контура 1431:

.

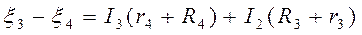Добавив к двум последним уравнениям условие равенства нулю алгебраической суммы сил токов в любой узловой точке (первое правило Кирхгофа), получим следующую систему уравнений:

Мы получили линейную систему из трех уравнений, она разрешима при наличии не более трех неизвестных величин.

Date: 2016-11-17; view: 897; Нарушение авторских прав