Уравнение состояния идеального газа. Изопроцессы в газах

Используя зависимость давления идеального газа от его температуры и концентрации молекул

,

можно найти связь между макроскопическими параметрами газа – объемом V, его давлением p и температурой Т. Учитывая, что концентрация молекул газа равна n=N/V, а число молекул N определяется произведением количества вещества ν на постоянную Авогадро N_а, получаем

.

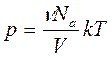Произведение постоянной Авогадро N_а на постоянную Больцмана k называется молярной газовой постоянной R (R≈8,31 Дж/(моль К)). Тогда

.

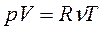Количество вещества ν можно найти, зная массу вещества m и его молярную массу М:

.

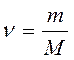Т.о., уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):

.

Уравнение Менделеева-Клапейрона показывает, что возможно одновременное изменение пяти параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближено как процессы, в которых изменяются лишь два параметра из пяти. Особую роль в физике и технике играют три процесса – изотермический, изохорный, изобарный. Рассмотрим эти процессы.

Изотермический процесс – процесс, протекающий при постоянной температуре Т. Из уравнения состояния идеального газа следует, что при постоянной температуре и неизменных значениях массы газа и его молярной массы произведение давления газа на его объем должно оставаться постоянным:

.

Данное уравнение было получено из эксперимента до создания молекулярно-кинетической теории газов в 1662 г. английским физиком Р.Бойлем и в 1676 г. французским физиком Э.Мариоттом. Поэтому это уравнение называют законом Бойля-Мариотта.

Изотермический процесс можно осуществить, например, путем изменения объема газа при постоянной температуре. График изотермического процесса называется изотермой. Изотерма, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается давление газа, а по оси абсцисс – его объем, является гиперболой (рис. 11, а).

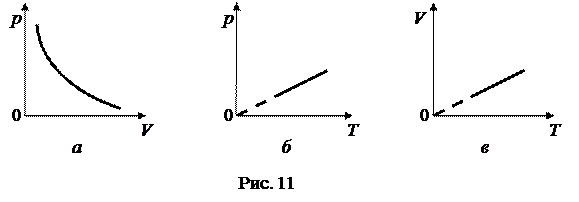
Изохорный процесс – процесс, протекающий при неизменном объеме и условии m=const и M=const.

При этих условиях из уравнения состояния идеального газа для двух значений температуры Т₀ и Т следует

.

Если Т₀ выбрать равным 273 К (0^о С), то обозначив

,

получим уравнение для изохорного процесса

,

где р – давление газа при абсолютной температуре Т, р₀ – давление газа при температуре 0^о С, α – температурный коэффициент давления газа.

График уравнения изохорного процесса называется изохорой. Изохора, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается давление газа, а по оси абсцисс – его абсолютная температура, является прямой, проходящей через начало координат (рис. 11, б).

Экспериментальным путем зависимость давления газа от температуры исследовал французский физик Ж.Шарль в 1787 г. Поэтому уравнение изохорного процесса называется законом Шарля.

Изохорный процесс можно осуществить, например, нагреванием воздуха при постоянном объеме.

Изобарный процесс – процесс, протекающий при неизменном давлении и условии m=const и M=const.

Таким же способом, как это было сделано для изохорного процесса, можно получить для изобарного процесса уравнение

,

где V – объем газа при абсолютной температуре Т, V₀ – объем газа при температуре 0^о С, α – температурный коэффициент объемного расширения газа.

График уравнения изобарного процесса называется изобарой. Изобара, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается объем газа, а по оси абсцисс – его абсолютная температура, является прямой, проходящей через начало координат (рис. 11, в).

Экспериментальное исследование зависимости объема газа от температуры провел в 1802 г. французский физик Ж.Гей-Люссак. Поэтому уравнение изобарного процесса называют законом Гей-Люссака. Изобарный процесс происходит, например, при нагревании или охлаждении воздуха в стеклянной колбе, соединенной со стеклянной трубкой, отверстие в которой закрыто небольшим столбом жидкости.

Реальный газ

Экспериментальные исследования свойств газов при высоких давлениях и низких температурах убедительно показали, что уравнение состояния идеального газа дает хорошее согласие с экспериментом для каждого исследуемого газа лишь при температуре выше некоторого значения, вполне определенного для каждого вещества, и при не очень высоких давлениях. Расхождение результатов теории и практики в области низких температур и высоких давлений газов свидетельствует о непригодности при этих условиях упрощенной модели строения газов, в которой не учитываются размеры молекул и силы взаимного притяжения.

В 1873 г. голландский физик И.Ван-дер-Ваальс показал, что согласие результатов теории и эксперимента в области высоких давлений и низких температур оказывается значительно лучшим, если учесть, что молекулы не только отталкиваются при соударениях, но еще и притягиваются друг к другу сравнительно слабыми силами на расстояниях, сравнимых с размерами молекул.

При движении молекулы вдали от стенок сосуда, в котором заключен газ, на нее действуют силы притяжения соседних с ней молекул, но равнодействующая всех этих сил в среднем равна нулю, так как молекулу со всех сторон окружает в среднем одинаковое число соседей. При приближении некоторой молекулы к стенке сосуда все остальные молекулы газа располагаются по одну сторону от нее, и равнодействующая всех сил притяжения оказывается направленной от стенки сосуда внутрь газа. Это приводит к тому, что уменьшается импульс, передаваемый молекулой стенке сосуда. В результате давление газа на стенки сосуда уменьшается по сравнению с тем, каким оно было бы в отсутствие сил притяжения между молекулами:

.

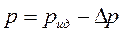Уменьшение импульса, переданного молекулой при ударе о стенку, пропорционально силе притяжения, действующей на нее со стороны ее ближайших соседей, т.е. пропорционально концентрации молекул. Полный же импульс, передаваемый всеми молекулами газа стенкам сосуда, в свою очередь пропорционален их концентрации. Поэтому вместо уравнения для идеального газа 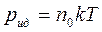для реального газа получим:

.

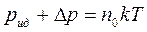Поскольку сила, действующая на одну молекулу, пропорциональна концентрации окружающих ее молекул, а суммарное давление также пропорционально концентрации, то дополнительное давление пропорционально квадрату концентрации, или, что то же самое, обратно пропорционально квадрату объема газа:

,

где а – постоянная, зависящая от вида газа. Учитывая это, для одного моля газа получим:

.

Это первая поправка, вводимая в уравнение Ван-дер-Ваальса.

Вторая поправка должна учесть тот факт, что при любых, даже сколь угодно больших давлениях объем газа не может стать равным нулю. В модели Ван-дер-Ваальса молекулы принимают за твердые шарики диаметром d. В этом случае оказывается, что молекулы реального газа свободно перемещаются не в объеме сосуда V, а в уменьшенном объеме

.

Здесь b – так называемый «запрещенный объем»; он равен

,

где N – общее число молекул газа.

Итак, получаем

, или иначе:

.

Это и есть уравнение Ван-дер-Ваальса для одного моля реального газа. Заметим, что если у идеального газа объем обратно пропорционален давлению и его изотерма в осях p, V – это гипербола, то у ван-дер-ваальсовского газа эта зависимость гораздо более сложна. График изотермы – кубическая парабола:

.

Хотя уравнение Ван-дер-Ваальса дает лучшее согласие теории с результатами эксперимента, все же точность расчетов, выполненных на его основе, обычно недостаточна для решения практических задач на уровне требований современной техники. Поэтому на практике приходится использовать уравнения состояния реального газа еще более сложного вида. Уравнение же Ван-дер-Ваальса интересно тем, что дает качественное объяснение основных отличий в поведении реального газа от идеального.

Date: 2016-11-17; view: 791; Нарушение авторских прав