Законы сохранения в механике

Основную задачу механики – определение положения тела в любой момент времени – можно решить с помощью законов Ньютона, если заданы начальные условия и силы, действующие на тело, как функции координат и скоростей (и времени). На практике эти зависимости не всегда известны. Однако многие задачи в механике можно решить, не зная значений сил, действующих на тело. Это возможно потому, что существуют величины, характеризующие механическое движение тел, которые сохраняются при определенных условиях. Если известны положение тела и его скорость в какой-то момент времени, то при помощи сохраняющихся величин можно определить положение и скорость этого тела после любого взаимодействия, не прибегая к законам динамики.

Сохраняющимися величинами в механических процессах являются импульс, момент импульса и энергия.

Закон сохранения импульса. Умножим выражение для второго закона Ньютона в виде (при действии постоянной силы) на Δt: . Величину называют импульсом тела (иначе – количеством движения), 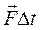– импульсом силы. Используя эти понятия, второй закон Ньютона можно сформулировать следующим образом: импульс приложенных к телу сил равен изменению импульса тела:

.

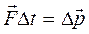В этой более общей формулировке не предполагается постоянство ни силы, ни массы. Именно в таком общем виде мы дальше будем понимать второй закон Ньютона – основное уравнение динамики.

При рассмотрении системы тел следует учесть, что каждое из них может взаимодействовать как с телами, принадлежащими системе, так и с телами, не входящими в эту систему. Пусть имеется система из двух материальных точек, взаимодействующих друг с другом внутренними силами и . Внешние силы, с которыми внешние тела действуют на эти точки, обозначим 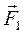и 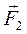(рис. 8).

Запишем второй закон Ньютона для каждой из материальных точек рассматриваемой системы для промежутка времени Δt:

;

.

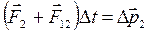Сложив оба равенства, получим:

.

По третьему закону Ньютона , следовательно, изменение импульса всей системы, равное векторной сумме изменений импульсов составляющих ее частиц, выглядит так:

.

Эту формулу можно обобщить для системы, состоящей из любого числа тел:

,

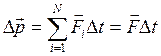где – векторная сумма внешних сил, действующих на рассматриваемую систему тел.

В инерциальных системах отсчета изменение полного импульса системы материальных точек равно импульсу внешних сил, действующих на эту систему.

Система тел, на которые не действуют внешние силы или сумма всех внешних сил равна нулю, называется замкнутой. Тогда из приведенного выше выражения следует закон сохранения импульса: в замкнутой системе тел импульс системы сохраняется. Этот вывод является следствием второго и третьего законов Ньютона.

Действительно, если , то , .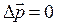

К незамкнутым системам тел закон сохранения импульса не применим; однако постоянными остаются проекции импульса на координатные оси, в направлении которых сумма проекций приложенных внешних сил равна нулю.

В неинерциальных системах отсчета при отсутствии взаимодействия тел скорость движения тел изменяется со временем. Поэтому импульс любого тела при отсутствии взаимодействия с другими телами не остается постоянным, если выбрана неинерциальная система отсчета. Следовательно, необходимым условием применимости закона сохранения импульса к замкнутой системе взаимодействующих тел является выбор инерциальной системы отсчета. В неинерциальных системах отсчета закон сохранения импульса несправедлив.

Закон сохранения момента импульса. Основное уравнение динамики вращательного движения тела под действием постоянного момента силы =const можно представить в виде:

,

откуда

.

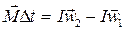Пользуясь законами Ньютона, можно доказать, что полученное уравнение справедливо и тогда, когда момент инерции тела изменяется. В этом случае уравнение динамики вращающегося тела в более общем виде запишется так:

.

Произведение момента инерции тела на угловую скорость его вращения называется моментом импульса:

.

Вектор момента импульса направлен в ту же сторону, что и вектор угловой скорости (если ось вращения проходит через ось симметрии тела).

Момент импульса – одна из важнейших характеристик вращательного движения тела. Когда суммарный момент сил, действующих на тело, относительно данной оси вращения равен нулю, то

.

Отсюда

.

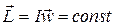Это и есть закон сохранения момента импульса. Закон сохранения момента импульса справедлив не только для одного тела, но и для любой замкнутой системы тел.

Замечательной особенностью вращательного движения является свойство вращающихся тел при отсутствии взаимодействий с другими телами сохранять неизменными не только момент импульса, но и направление оси вращения в пространстве. Неизменным ориентиром для путешественников на поверхности Земли служит Полярная звезда. Примерно на эту звезду направлена ось вращения Земли, и кажущаяся неподвижность Полярной звезды на протяжении столетий наглядно доказывает, что в течение этого времени направление оси вращения Земли в пространстве не изменилось. Но если точно измерять момент импульса в течение длительного времени, то окажется, он все же поворачивается. За 26 тысяч лет момент опишет коническую поверхность вокруг полюса эклиптики и вернется почти к начальному положению (прецессия земной оси). Прецессия возникает в результате неравномерного гравитационного притяжения к Луне экваториального уширения земной фигуры.

Все известные нам планеты, все их спутники вращаются. Существует некая закономерность во вращении планет: чем больше масса планеты, тем быстрее она вращается (хотя из этого правила есть исключения). Разгадка этой закономерности скрыта в истории образования Солнечной системы. По современным представлениям Солнце и планеты образовались из вращающейся туманности, состоящей из газа и твердых пылевых частиц. При столкновениях частицы укрупнялись, образуя зародыши планет и Солнца. Наибольшее число столкновений происходило в центре масс системы, туда же собрался и почти весь газ туманности. Так образовалось Солнце. Однако почти весь начальный момент импульса туманности оказался сосредоточенным не в Солнце, а в планетах. После того как Солнце зажглось, под воздействием его излучения легкие газы из ближайшей окрестности Солнца были рассеяны на периферию. Там из них образовались планеты-гиганты. Планеты же земной группы оказались составленными в основном из вещества твердых частиц. При сжатии вещества вращающейся туманности в плотные шары планет скорость вращения возрастает – это следствие закона сохранения момента импульса. Поэтому неудивительно, что у планет-гигантов и скорость вращения оказалась больше, чем у меньших по размерам планет.

Закон сохранения энергии в механических процессах. Если на тело действует постоянная сила , составляющая постоянный угол 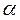с перемещением тела 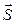, то работа этой силы определяется как произведение модулей силы и перемещения на косинус угла между векторами силы и перемещения, т.е. как скалярное произведение вектора силы на вектор перемещения:

.

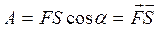Единица работы в СИ – джоуль (Дж) – равна работе, совершаемой силой в 1 Н на перемещении 1 м вдоль направления действия силы.

Если на тело действует переменная сила, то, чтобы вычислить ее работу, нужно перемещение разбить на малые участки 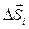и найти сначала элементарную работу: 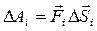, а затем полную работу как предел суммы элементарных работ:

,

где М₁ и М₂ – начальная и конечная точки перемещения.

Графически работа определяется по площади криволинейной трапеции, как показано на рисунке 9.

На оси абсцисс откладывается в определенном масштабе модули перемещения, на оси ординат проекции силы (также в соответствующем масштабе). Тогда площадь трапеции численно равна работе силы.

Выразим работу силы через начальную и конечную скорости тела, движущегося под действием этой силы. Для этого рассмотрим простейший случай действия постоянной силы вдоль перемещения. Подставив в формулу 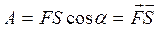выражения для силы и перемещения , получим:

.

Величину для материальной точки называют кинетической энергией E_k.

Полученный результат называют теоремой о кинетической энергии. Теорема о кинетической энергии верна для сил любой природы, в том числе и для переменных. Если на тело действует несколько сил, то под А следует понимать работу векторной суммы всех сил.

Теорема о кинетической энергии справедлива для любой инерциальной системы отсчета. Вместе с тем следует учесть, что кинетическая энергия и работа силы являются относительными величинами, зависящими от выбора системы отсчета.

Кинетической энергией обладают не только тела, движущиеся поступательно, но и любые вращающиеся тела. Формула для кинетической энергии вращающегося тела записывается в виде:

.

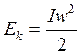В практике часто встречаются случаи, когда тело одновременно вращается и в то же время перемещается в плоскости, перпендикулярной оси вращения. Такое движение называется плоским. Например, качение цилиндра или шара по плоскости является примером плоского движения. Полная кинетическая энергия твердого тела в этом случае равна сумме кинетической энергии поступательного движения и кинетической энергии вращения вокруг оси, проходящей через центр масс:

,

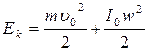где I₀ –моментинерции тела относительно оси, проходящей через его центр масс, υ₀ – скорость движения центра масс тела направленная перпендикулярно оси вращения.

Выше мы показали, что работа силы определяется разностью конечного и начального значений кинетической энергии. При этом кинетическая энергия зависит только от состояния движения тела – его скорости, и не зависит от того, с помощью какого процесса тело пришло в состояние движения с этой скоростью.

Но кроме кинетической энергии есть еще один вид энергии – потенциальная. Потенциальной энергией взаимодействующих тел называется энергия, зависящая от взаимного расположения этих тел.

Нетрудно показать, что работа сил тяжести, тяготения, упругости не зависит от формы траектории, а определяется только положениями начальной и конечной точки. Такие силы называют консервативными.

;

;

.

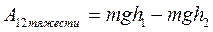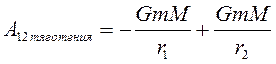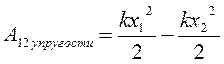
Введем понятие потенциальной энергии как некоторой функции состояния взаимодействующих тел (их взаимного расположения) и будем считать, что работа консервативной силы равна убыли потенциальной энергии:

.

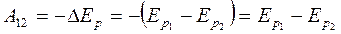Тогда оказывается, что потенциальная энергия тела в поле тяжести равна

.

Потенциальная энергия в поле тяготения равна

.

А потенциальная энергия деформированной пружины равна

.

Заметим, что потенциальная энергия является функцией координат точек, в которых расположены взаимодействующие тела. Значение произвольной постоянной в формулах зависит от выбора нулевого уровня потенциальной энергии. Изменение потенциальной энергии от выбора нулевого уровня не зависит.

Если в замкнутой системе действуют только консервативные силы, то работа, совершаемая этими силами, равна взятому с противоположным знаком изменению потенциальной энергии тел:

.

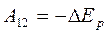С другой стороны, работа этих же сил равна изменению кинетической энергии системы тел:

.

Из сравнения этих формул получаем выражение

,

которое представляет собой закон сохранения полной механической энергии:

.

Полная механическая энергия сохраняется только в таких замкнутых системах, в которых действуют лишь консервативные силы.

В общем случае, когда в системе действуют силы, зависящие от скорости, например, силы трения (такие силы называются диссипативными) и силы, зависящие от времени (их называют нестационарными), то полная механическая энергия не сохраняется.

Энергетика бега. Предположим, что предмет передвигается с постоянной скоростью по горизонтальной поверхности. Работа, которая при этом совершается, сводится к преодолению трения и сопротивления воздуха. При беге действие трения невелико, но, тем не менее, бег с постоянной скоростью связан со значительными затратами энергии. Энергия тратится на движения бегуна вверх-вниз и на отталкивание ногами от почвы. Кроме того, тело бегуна превращает энергию в теплоту. Дополнительная причина потери энергии заключается в том, что ноги бегуна, масса которых составляет приблизительно 50% от массы тела, в процессе бега постоянно ускоряются и тормозятся. Поэтому работа, выполняемая мышцами ног для поддержания движения тела вперед с постоянной скоростью, велика.

Работа, выполняемая ногами бегуна, равна

,

где F – сила мышц, d – расстояние, на котором при каждом шаге мышцы выполняют работу, а т – масса ног. Известно, что сила мышц пропорциональна квадрату характеристической длины L (высоты человека). Дело в том, что все мышцы состоят из пучков мышечных волокон. Эти волокна почти одинаковы и упакованы с равной плотностью в мышцах различных организмов. Сила мышц в некотором приближении прямо пропорциональна числу волокон в мышце, приходящихся на единицу площади поперечного сечения. Площадь мышц организма, опять же в некотором приближении, прямо пропорциональна характерному поперечному сечению, которое равно квадрату характеристической длины.

Кроме того, расстояние d пропорционально L, а масса пропорциональна L³. Следовательно,

.

Таким образом, скорость, которую может поддерживать бегун, не зависит от его размеров. В действительности этот анализ относится не только к человеку. Все животные с аналогичными формами будут иметь сравнимые скорости бега независимо от размеров.

Люди – плохие бегуны, поскольку их движение обеспечивается мышцами, целиком сосредоточенными в ногах, – слишком велика масса, которая должна быть ускорена и заторможена. Самые быстроходные животные имеют тонкие ноги, а основная мышечная масса сосредоточена у них в теле.

Если бы скорости бега были приблизительно независимы от размеров животных, природный баланс между охотником и добычей нарушился бы. Заметим, что волк и заяц имеют почти одинаковые скорости бега, что верно и в случае гепарда и газели.

Глава 2

ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ

Date: 2016-11-17; view: 697; Нарушение авторских прав