Вращательное движение тел

Кинематика вращательного движения. Вращательным движением называется такое движение тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а плоскости окружностей перпендикулярны оси вращения. Вращается вокруг своей оси планета Земля, вследствие чего происходит смена дня и ночи, вращаются роторы турбин, шестерни и валы во всевозможных станках и машинах.

Сложные движения можно рассматривать как сочетание поступательного и вращательного движений. Движение колеса автомобиля, например, складывается из вращения колеса вокруг своей оси и поступательного движения оси относительно дороги.

При вращении твердого тела вокруг неподвижной оси линейные скорости и ускорения для разных точек различны. Поэтому такое движение характеризуется угловыми величинами, одинаковыми в данный момент времени для всех точек вращающегося тела.

Мгновенная угловая скорость равна производной от угла поворота по времени:

; .

Угловую скорость принято рассматривать как вектор, направленный вдоль оси вращения по правилу правого винта: если винт вращать в том же направлении, как вращается тело, то направление движения винта совпадает с направлением угловой скорости (рис. 5).

Угловая и линейная скорости точки связаны соотношением:

,

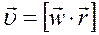где r – радиус окружности, по которой вращается точка.

Если тело за любые равные промежутки времени поворачивается на одинаковые углы, то такое движение называют равномерным вращательным движением.

Используя понятие угловой скорости, можно дать еще одно определение равномерному вращательному движению. Равномерным вращательным движением называют движение с постоянной угловой скоростью (w=const). Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси (w=7,292•10^-5 с^-1).

Равномерное вращательное движение встречается сравнительно редко. Гораздо чаще приходится иметь дело с вращательным движением, при котором угловая скорость с течением времени изменяется. Для описания неравномерного вращательного движения надо ввести величину, которая характеризовала бы изменение угловой скорости. Такой величиной является м гновенное значение углового ускорения равное производной угловой скорости по времени:

; .

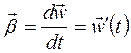При ускоренном вращении векторы и совпадают по направлению; при замедленном вращении вектор направлен противоположно вектору .

Связь линейного ускорения точки с ее угловым ускорением:

,

где r – радиус окружности, по которой вращается точка.

Момент силы. Опыт показывает, что результат действия силы на тело, вращающееся вокруг оси, зависит не только от значения силы, но и от того, где эта сила приложена к телу.

Пусть к телу, вращающемуся вокруг оси, в некоторой точке А приложена сила , лежащая в плоскости, перпендикулярной оси (рис. 6). Разложим эту силу на две составляющие и – вдоль радиуса вектора и перпендикулярно ему. Составляющая не может изменить характер движения тела; составляющая сообщает телу угловое ускорение.

Моментом силы будем называть вектор , направленный вдоль оси вращения и ориентированный по правилу правого винта относительно вектора силы. Модуль момента силы равен

,

где – плечо силы. Оно равно кратчайшему расстоянию между осью вращения и направлением действия силы.

Основное уравнение динамики вращательного движения твердого тела. Чтобы получить искомое уравнение, рассмотрим вначале простейший случай, когда материальная точка массой m вращается на невесомом твердом стержне длиной r вокруг оси (рис. 7).

Второй закон Ньютона для этой точки запишется так:

.

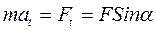Но тангенциальное ускорение

.

Подставив в предыдущую формулу, получим:

.

Умножив обе части этого равенства на r,чтобы свести действие силы к ее моменту, будем иметь:

.

Произведение массы точки на квадрат ее расстояния до оси назовем моментом инерции материальной точки относительно оси:

; .

Тогда,

.

Поскольку векторы 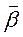и направлены в одну и ту же сторону вдоль оси вращения, то данное выражение можно записать в векторном виде:

.

Это и есть основное уравнение динамики вращательного движения. Оно у нас получено для одной точки, но легко обобщается на вращающееся твердое тело. В самом деле, твердое тело можно рассматривать как совокупность частиц с массами m₁, m₂, m₃,…., m_n, расположенных на расстояниях r₁, r₂, r₃, …, r_n от оси вращения. Так как все эти точки вращаются с одинаковым угловым ускорением, то, суммируя систему уравнений , написанных для всех частиц, получим:

,

где – сумма моментов внутренних сил, – сумма моментов внешних сил. Но сумма моментов внутренних сил равна нулю, и остается только сумма моментов внешних сил.

Моментом инерции тела назовем сумму моментов инерции составляющих его частиц:

.

Обозначив сумму моментов внешних сил через , увидим, что уравнение применимо и к любому вращающемуся твердому телу.

Основное уравнение динамики вращающегося твердого тела аналогично второму закону Ньютона. В самом деле, ускорение материальной точки пропорционально сумме сил и обратно пропорционально ее массе; угловое ускорение вращающегося твердого тела пропорционально сумме моментов сил и обратно пропорционально моменту инерции тела.

Однако имеется и принципиальная разница. Если масса тела является инвариантом и не зависит от того, как тело движется, то момент инерции тела зависит от того, вокруг какой оси оно вращается. При изменении положения оси вращения или ее направления в пространстве значение момента инерции меняется. В таблице 1 приведены формулы для вычисления моментов инерции некоторых тел относительно оси, проходящей через центр масс этих тел.

Таблица 1

Тело	Ось вращения проходит	Момент инерции
Обруч	через центр обруча перпендикулярно плоскости обруча	mR2
Диск (цилиндр)	через центр диска перпендикулярно плоскости диска	0,5 mR2
Диск	через центр диска вдоль его диаметра	0,25 mR2
Шар	через центр шара	0,4 mR2
Стержень длиной L	через середину тонкого стержня перпендикулярно ему	1/12 mL2

Date: 2016-11-17; view: 635; Нарушение авторских прав