Основное уравнение кинетической теории идеального газа

В 1857 г. немецкий физик Р. Клаузиус, используя модель идеального газа, впервые систематически изложил кинетическую теорию газов. Он ввел понятие о средних величинах, длине свободного пробега молекул, вычислил давление газа на стенки сосуда и среднюю длину пути между двумя столкновениями молекул.

Идеальным Клаузиус назвал газ, удовлетворяющий следующим условиям:

1) объемом всех молекул газа можно пренебречь по сравнению с объемом сосуда, в котором этот газ находится;

2) время столкновения молекул друг с другом пренебрежительно мало по сравнению со временем между двумя столкновениями (т.е. временем свободного пробега молекулы);

3) молекулы взаимодействуют между собой только при непосредственном соприкосновении, при этом они отталкиваются;

4) силы притяжения между молекулами идеального газа ничтожно малы, и ими можно пренебречь.

Исходя из этих положений, Клаузиус вывел все свойства идеального газа и установил соотношения между его микроскопическими и макроскопическими параметрами.

Микроскопическими параметрами газа называют индивидуальные характеристики молекул (масса молекулы, ее скорость, импульс, кинетическая энергия поступательного движения). Параметры газа как физического тела называются макроскопическими (температура, объем, давление газа). Одной из важнейших задач молекулярно-кинетической теории было установление связи между макроскопическими и микроскопическими параметрами газа.

Выведем основное уравнение для случая, когда газ находится в сосуде кубической формы. Это делается только ради упрощения расчета. Вообще же основное уравнение МКТ можно вывести для газа, находящегося в сосуде любой формы и даже при отсутствии всякого сосуда.

Пусть в кубическом сосуде с ребром а находится идеальный газ, состоящий из N молекул; масса каждой молекулы m₀. Ввиду полной хаотичности движения молекул результат их действия на стенки сосуда будет таким же, как в случае, если бы 1/3 всех молекул двигалась прямолинейно между передней и задней стенками сосуда, 1/3 – между правой и левой и 1/3 – между верхней и нижней. Поэтому допустим, что число молекул, движущихся в каждом из трех взаимно перпендикулярных (и перпендикулярных к соответствующим стенкам) направлений, равно N=1/3 N*.

Проследим мысленно за одной из молекул, летящей со скоростью υ в направлении правой стенки сосуда. Долетев до стенки, молекула ударит в нее, отскочит назад, полетит к левой стенке, ударит в нее и т.д. Обозначим силу удара молекулы о стенку через Δf, а продолжительность времени удара – через Δt. Тогда импульс силы, сообщенной молекулой стенке при ударе, равен Δf Δt.

Согласно закону изменения импульса, импульс силы равен изменению импульса тела:

.

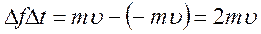Знак минус показывает, что скорость при ударе изменяет направление на противоположное.

Молекула действует на правую стенку с силой Δ f кратковременно, только в моменты ударов; остальную и притом большую часть времени между ударами она не действует на эту стенку. Поэтому средняя сила Δ f_ср действия молекулы на правую стенку за одну секунду значительно меньше фактической силы Δ f. Очевидно, что импульс средней силы равен сумме импульсов всех сил Δ f, действующих на стенку в течение одной секунды:

,

где k – число ударов молекулы в правую стенку за одну секунду. Число k равно перемещению молекулы за 1 с,деленному на перемещение 2а, совершаемое ею между двумя последовательными ударами в правую стенку. Так как перемещение молекулы за одну секунду численно равно скорости υ, то k= υ/2a. Тогда средняя сила

.

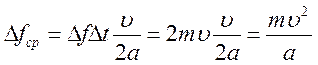Учитывая, что на правую стенку сосуда действуют и все другие (N*) молекулы газа, найдем полную силу f, с которой газ действует на правую стенку:

,

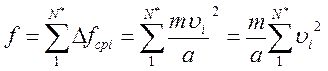где υ _i= υ ₁, υ ₂,…, υ _N^* – скорости молекул.

Разделим и умножим правую часть равенства на N*:

.

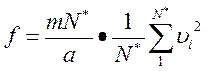Нетрудно установить, что выражение 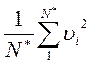представляет собой квадрат средней квадратичной скорости молекул (квадратный корень из суммы квадратов отдельных значений величины, деленной на их число), которую мы обозначим через u. Тогда

.

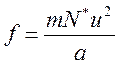Разделим обе части последнего равенства на а² и заменим N* на 1/3 N:

.

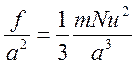Но а²=S – площадь правой стенки сосуда, а а³=V – объем сосуда. Тогда

.

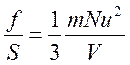Очевидно, что f/S=p – давление газа на правую стенку, а N/V=n₀ – число молекул в единице объема газа. Поэтому

.

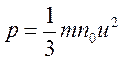Разделив и умножив правую часть этого равенства на 2, получим

,

где mυ²/2=W_ср – средняя кинетическая энергия поступательного движения одной молекулы. Следовательно,

.

Очевидно, что совершено такое же выражение получится и для давления газа на каждую из остальных стенок сосуда. Это и есть основное уравнение кинетической теории идеального газа (уравнение Клаузиуса). Основное уравнение показывает, что давление газа прямо пропорционально средней кинетической энергии поступательного движения молекул, содержащихся в единице объема газа.

Температура

Основное уравнение МКТ для идеального газа устанавливает связь легко измеряемого макроскопического параметра – давления – с такими микроскопическими параметрами газа, как средняя кинетическая энергия и концентрация молекул. Но, измерив только давление газа, мы не можем узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужны измерения еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура.

Через некоторое время после установления контакта между телами изменения макроскопических параметров тел прекращаются. Такое состояние тел называется тепловым равновесием. Физический параметр, одинаковый во всех частях системы тел, находящихся в состоянии теплового равновесия, называется температурой тела. В повседневной практике наиболее распространен способ измерения температуры с помощью жидкостного термометра. Существенным недостатком данного способа является то, что шкала температуры при этом оказывается связанной с конкретными физическими свойствами определенного вещества, используемого в качестве рабочего тела в термометре (ртути, глицерина, спирта…).

Для того чтобы найти более совершенный способ определения температуры, нужно найти такую величину, которая была бы одинаковой для любых тел, находящихся в положении теплового равновесия.

Экспериментальные исследования свойств газов показали, что для любых газов, находящихся в состоянии теплового равновесия, отношение произведения давления газа на его объем к числу молекул оказывается одинаковым:

.

Этот опытный факт позволяет принять величину θ в качестве естественной меры температуры. С учетом основного уравнения МКТ

.

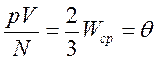Следовательно, средняя кинетическая энергия молекул любых газов, находящихся в тепловом равновесии, одинакова. Величина θ выражается в джоулях. Температуру же принято измерять в градусах. Принимая, что температура Т в градусах и величина θ связаны уравнением

,

где k – коэффициент пропорциональности, зависящий от выбора единицы температуры, получаем

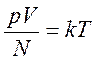или .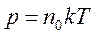

Последнее уравнение показывает, что имеется возможность выбрать температурную шкалу, не зависящую от природы газа, используемого в качестве рабочего тела (абсолютная шкала). Ее предложил английский физик У.Кельвин, поэтому шкалу называют также шкалой Кельвина. Единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия. Температура 0⁰С по шкале Цельсия соответствует температуре 273 К по абсолютной шкале. Абсолютная температура Т может быть только положительной или равной нулю. Температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю, называется абсолютным нулем температуры. Коэффициент k=1,38•10^-23Дж/К называется постоянной Больцмана, в честь Л.Больцмана, одного из создателей МКТ.

Сопоставляя уравнения 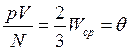и , получаем

.

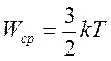Т.е, средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре.

Date: 2016-11-17; view: 543; Нарушение авторских прав