Краткие теоретические сведения

Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Записывается: A .

Матрица записывается в виде или, сокращенно, , где i = 1, 2, 3, …, m – номер строки, j = 1, 2, 3, …, n – номер столбца.

Числа , составляющие матрицу, называются ее элементами.

Матрица называется квадратной n- го порядка, если число ее строк равно числу столбцов и равно n.

Элементы называются диагональными и образуют главную диагональ квадратной матрицы A.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Единичная матрица обозначается буквой E.

Матрица, полученная из данной матрицы заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной матрице. Обозначается .

Суммой двух матриц A = и B = называется матрица C = такая, что (i = 1, 2, …, m; j = 1, 2, …, n).

Разностью двух матриц A = и B = называется матрица C = такая, что (i = 1, 2, …, m; j = 1, 2, …, n).

Произведением матрицы A = на число k называется матрица B = такая, что (i = 1, 2, …, m; j = 1, 2, …, n).

Произведением матрицы A = на матрицу B = называется матрица C = такая, что (i = 1, 2, …, m; k = 1, 2, …, p).

Определителем квадратной матрицы второго порядка A = называется число = .

Определителем квадратной матрицы третьего порядка A = называется число = = .

Минором элемента определителя n-го порядка называется определитель n- 1 - гопорядка, полученный из исходного определителя вычеркиванием i – той строки и j-го столбца.Минор элемента обозначается: .

Алгебраическим дополнением элемента определителя называется число .

Матрицей, союзной к матрице A, называется матрица

= ,

где – алгебраические дополнения элементов определителя матрицы A.

Матрица называется обратной к матрице A, есливыполняется условие: , где E – единичная матрица того же порядка, что и матрица A.

Обратная матрица к матрице A, находится по формуле: , где - матрица, союзная к транспонированной матрице .

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

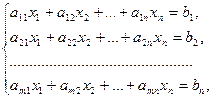(1)

где - неизвестные, числа - коэффициенты системы, - свободные члены.

Матрица называется основной матрицей системы линейных уравнений (1).

Матрица называется расширенной матрицей системы линейных уравнений (1).

Решением системы (1)называется n значений неизвестных , при подстановке которых в систему (1) каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система уравнений называется несовместной, если она не имеет ни одного решения.

Совместная система уравнений называется определенной, если она имеет единственное решение.

Совместная система уравнений называется неопределенной, если она имеет более одного решения.

Решить систему уравнений – это значит выяснить, совместна она или несовместна и в случае, если система совместна, то найти все ее решения.

Две системы уравнений называются равносильными, если они имеют одно и то же множество решений.

Равносильные системы линейных уравнений получаются при элементарных преобразованиях системы.

К элементарным преобразованиям системы линейных уравнений относятся:

- перестановка местами двух уравнений системы;

- умножение уравнения системы на ненулевое число;

- замена какого-то уравнения системы на сумму этого уравнения и другого уравнения системы, умноженного на какое-либо число;

- удаление из системы линейных уравнений уравнения вида .

К основным методам решения систем линейных уравнений относятся:

- Метод Крамера;

- Матричный способ (метод обратной матрицы);

- Метод Гаусса.

Метод Крамера применяется в случае, когда число уравнений в системе (1) и число неизвестных равны, то есть m = n, при этомD = det A 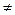0. Тогда для нахождения решения системы линейных уравнений применяются формулы Крамера:

x = , где j = 1; 2; 3.

Здесь: D = det A, а D _j – определитель матрицы, получаемой из матрицы системы заменой столбца j столбцом свободных членов.

Метод обратной матрицы применяется также для случая, когда число уравнений в системе (1) и число неизвестных равны, то есть m = n, при этом

D = det A 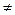0.

Тогда для нахождения решения системы линейных уравнений применяется формула

X = A ·B.

В данной формуле: X = - столбец неизвестных, B = - столбец свободных членов, а

.

Метод Гаусса (метод последовательного исключения неизвестных) применяется для любых систем линейных уравнений. Он состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы. При этом на практике все преобразования на первом этапе совершаются над расширенной матрицей системы линейных уравнений (1).

Date: 2016-11-17; view: 326; Нарушение авторских прав