Лшемділіктің фракталдық эволюциясы

Астрофизикалық мәліметтер қатарында алмаспалы құрылымға ие тербелістер байқалады. Алмасу –тұрақты және тұрақты емес тербелістердің жүйелі түрде алмасуы.

Осыған ұқсас алмаспалы процесстер сызықты емес, тепе теңдігі жоқ, ашық жүйелерде жүзеге асады. Яғниөзұйымдықтың пайда болуына себепті жағдайлардың жасалуы. Озұйымдық процессі өзұқсас динамикалық қасиеттерге ие. Оның фазалық бейнесі ғажап (фракталды) аттрактор бола алады.

Уақыт бойынша эволюцияны қарастырайық x(t)– фракталдық өлшемдікпен байланысты (өлшенетін жиынтықпен сипатталатын аддитивті шама), кейбір функция модулі:

, (2.11)

осында -t мәнінің жиынтығының статистикалық сипаттамасы. Оны енгізу туындасын шектейтін Лифшиц–Гельдер шартын қанағаттандыру мақсатымен байланысты. Салыстырмалы өсімше модулін (x(t) мөлшерін өлшеу маштабы)фракталдық өлшемділік шартына сәйкс [55] алмастырамыз:

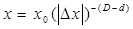, , , (2.12)

бұл жерде, фракталды емес тұрақты өлшемділік, - мәндер жиынының фракталдық өлшемділігі,d-топологиялық өлшемділік. (2.12)формуласын(2.11)формуласына қойып дискретті айырмаға өтеміз. Белгілік функцияның дискретті түрін арқылы белгілейміз. Әрқашанда болуына сәйкес,  дан тәуелді Оның дискретті i айнымалысы бойынша өзгерісін келесі түрде анықтаймыз:i айнымалысы бойынша өзгерісін келесі түрде анықтаймыз:

, (2.13)

Әдетте мәні ұйытқулар эволюциясынсызықты сипаттауға қолданылады. Біз 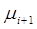ді арқылы анықтап, бұл шама модуліне шек қоймаймыз.

(2.12),(2.13)формулаларын ескеріп (2.11)формуласын жағдайы үшін келесі түрде жазамыз:

.14)14)

(2.14) формуласында,уақыттың бірдей мезеттерін таңдау мүмкін болуы үшін шамасын ескермейміз.Дискретті есептеу алгоритмі бойынша деп алудың алдында, біз мәнін арқылы модельдейміз:себебі осы ғана шама мәндерінің хаотизациясына сәйкес келеді.

шамасын енгізу мәнікелесі шарты қанағаттандыруда екенін ескереміз.

, (2.15)

осында,τ–процесстің сипатты уақыты.

кезінде, біз есептеуді , болатын өлшемділіктің Риман бойынша есептелу жағдайына келер едік. Ал деп таңдап алсақ, ның 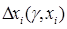функциясының өсімшесіне тәуелділігін ескере отырып, өлшемділіктің Лебег бойынша есептелуіне келеміз:

(2.16)

бұл жерде -кейбір тұрақты сан. ның мәнін сигнал спектірін сипаттауға арналған, сигнал базасының (күрделігінің) аналогы ретінде түсіндіруге болады:

, (2.17)

осында, -корреляцияның сипатты уақыты, -жиеліктер енділігі.Анықтамаға сәйкес хаостық сигналды сипаттау үшін таңдалған дәлдік күрделігін сипаттайды.Фракталдық объетінің өлшемділігі бақылайу дәлдігіне тәуелді, сондықтан да теория нәтежесіне тұрақтысы енеді. шамасының мәні процессті бақылауға таңдалған және т.с.с дәлдіктің дәрежесіне сәйкес келеді. Егер де туынды таңбасы (2.11)формулада сыртқы шарттармен анықталса (шуыл тәріздес әсерлер),ал(2.15) формулада , абсолют мәндері таңдалады.

деп,(2.14)теңдікті келесі түрде көшіріп жазамыз:

. (2.18)

(3.18) өрнекті дифференциалдап:

. (2.19)

аламыз. (2.18)және(2.19)формулалар ізделіп отырған алмасудың бейнелеуін береді.

Қарастырылып отырған 𝛾айнымалысының мәні, физикалық шама мәндерінің фракталдық өлшемділігінің бөлшек бөлігін сипаттау.

Көрсетілген бейнелеу, алмаспалы, хаостық эволюциялық процесстерді сипаттайды. Басқа белгілі моделдермен салыстырғанда, бұл бейнелеу Маңыздысы сол, тек осындай сигналдардың өзеріктілік критериларына сай болуы. Мұндай сигналдар ертеректе схемотехникалық, фазасы басқарылатын радиотехникалық арқылы физикалық эксперименттерде теория жүзінде алынған болатын. Шынайылыққа сәйкестігі физикалық негізделген болып табылады. Процестің фракталдылығы, оны бейнені шығаруда пайдалану өзерікті жүйелердің негізгі қасиеті болып табылады. Динамикалық хаос генераторының теңдеулер жүйесінде селективті контур жиілігінің кері байланыс фазасынан бейсыздық тәуелділігі алынды. Бұл фактор да өзеріктіліктің негізгі факторларының бірі болып табылады.

Date: 2016-05-25; view: 875; Нарушение авторских прав