Галактикаларды бейнелеулер арқылы модельдеу

Бейнелеу уақытқа байланысты динамикалық жүйе қасиеттерінің өзгерісінің графикалық көрінісі –жүйе элементтерінің әрқайсысы үшін уақыт пен кеңістікке сәйкес функционалды тәуелділігі бар жүйе. Бұл математикалық абстракция кез келген жүенің уақытқа байланысты эволюциясын зерттеуге не сипаттауға мүмкіндік береді.

Динамикалық жүйе күйі уақыттың кез келген мезетінде күй кеңістігінде нүктеге сәйкес заттық сандардың көптілігімен сипатталады. Динамикалық жүйенің эволюциясы детерменделген функциямен сипатталады. Яғни берілген уақыт интервалынан кейін, осыған дейінгі күйіне сәйкес, жүйе нақты, келесі күйге ие болады.

Динамикалық жүйе деп, қандай да бір объект, процесс немесе уақиғаның матиматикалық моделі ретінде түсінеміз.

Осымен қатар, динамикалық жүйе нақты күйге ие болатын жүйе ретінде елестетуге болады.Айтылған бойынша,динамикалық жүйе – жалпы кез келген жүйенің бір күйінене екінші күйне өту процесін сипаттайды.Фазалық кеңістіктегі бейнелеу —динамикалық жүйенің барлық мүмкін бола алатын күйлерінің жиынтығы.Осылайша,динамикалық жүйе өзінің бастапқы күйі мен келесі күйіне өтуін қамтамасыз ететін заңдар және олардың жиынымен сипатталады.

Динамикалық жүйе(уақыт бойынша дискретті де, үздіксіз де), кез-келген облыста беріліп, осы жерде бар болу теоремасы мен дифференциалды өрнектің жалғыз шешімі болу шартын қанағаттандыратын, дифференциалды теңдеулердің автономды жүйесімен сипатталады.Динамикалық жүйенің тұрақтылық күйлеріне дифференциалды теңдеудің айрықша нүктелері сәйкес келеді. Албұл жүйенің периодты шешімдері сәйкесінше тұйықталған фазалық қисықтармен сипатталады.

Қазіргі таңдағы бұл ғылымның атауына математиканың барлық салаларында кездесетін, солардың ішінде:топологияменалгебра,алгебралық геометрия, өлшемділік теориясы,дифференциалдық формалар теориясы,ерекшеліктер мен апаттар теориясы аппараттарын эффективті де ұтымды қоданып, физикалық заңдылықтарды түсіндіруді жүзеге асыратын әдістемелердің жалпылама жиыны тән [49,50]

Фракталдар.

Табиғаттакездесетінөлшемдеріатомдықмасштабтанәлемдіккеңістіккедейінсозылыпжатқанобьектілердің(нысандардың)геометриясыбіздіңонызерттептүсінуүшінқұратын,идеалдандырылғанмодельдеріміздебастыорыналады.Бірақдәстүрбойыншатабиғатгеометриясыниндуктивтітүсінудіңнегізіретіндеосыуақытқадейіневклидтікгеометрияныңтүсініктері:сызықтар,шеңберлер,сфераларментетраэдрларқолданылады.

Күрделіжүйелердеболатынпроцестерді,құрылымды–стохастикалыққұбылыстардыбарыншақарапайымтүрдесипаттауға,түсінументүсіндіругемүмкіндікберетінғылым–фракталдартеориясы.

Фракталтүсінігіалғашматематикалықтүрдекүрделігеометриялықформалардысипаттауүшіненгізіледі.Ғылымныңдамуыжәнекомпьютерліктехниканықолданудыңалуантүрлімүмкіндіктеріфракталтүсінігініңтабиғаттыңеңжалпы,түбегейлізаңдылықтарыменбайланыстыекенінкөрсетті.Физика–математикағылымдарыныңбұлжаңабағытыныңкүртдамуынафранцузғалымыБ.Мандельброттың1982жылыжарықкөрген"Табиғаттыңфракталдықгеометриясы"аттыкітабыныңшығуытікелейсебепболды.[51]

Б.Мандельбротбұлкітабындатабиғаттакездесетінфракталдықнысандардыңкөптегенмысалдарынкелтірдіжәнеоғанғылымикөпшіліктіңжаппайназарынаударды.Оныңдамытқангеометриясысантүрліобьектілердіңформасынсипаттауғақолданылуыменқатар,заңдылығыбар,масштабты–инвариантықұрылымдарныңмоделінсалуғамүмкіндікбереді.Осыүлгілердіқолдануретсізқұрылымдардызерттепбілудіңжаңажолдарыболыптабылды.

Аспандағыбұлттар,таусілемдері,терезешынысынақатқанқыраулар,полимердітүзетінмолекулар,тіріклеткаларжәнетағысолсияқтынысандарменқұрылымдардыңбәрінеортақбірқасиеті–олардыңкішіжәнебөліктерініңбір–бірінеұқсастығы.Әртүрліуақытмезетіндетүсірілген,үлкенжәнекішібұлттардыңсуреттерінсалыстыруолардыңөзгерузаңдылығыныңбірдейболатынынкөрсетеді.Осысияқтызаңдылықтыәртүрлімасштабтатүсірілгенжағалаусызықтарыныңфрагменттерінін(мысалы,Британияаралының,Аралтеңізінің,Балқашкөлінің)салыстыруарқылыдабайқауғаболады.

ОсындайөзұқсаснысандарүшінфранцузматематигіБ.Мандельбротжаңафрактал(латыншаданаудармасы–бөлшектік,кескіленген)ұғымыненгізді.Олқұрылымдық,өзіне-өзіұқсасиерархиялықішкіқұрылысыбаробьектілердіфракталдардепаталады.Фракталдыққасиетбейсызықпроцестерменқұбылыстардысипаттайтынфазалықкеңістіктерде,күрделіжүйеніңфункционалдыхаракеттерінде,адрондардыңәсерлесуінің,қоғамныңэкономикалықкөрсеткішініңөзгерістеріндежәнет.б.байқалады.[52,53]

Фракталдардыңдәлжәнеқатаңанықтамасыәзіргежоқ.Б.Мандельброталғашретфракталанықтамасыныңмынадайвариантынұсынған:фракталдептұтаскүйінебелгілібірмағынадаұқсасбөліктердентұратынқұрылымайтылады.

Математикадаөзұқсасгеометриялықобьектілердепбір-біріұқсас,санышектібірдейэлементтергебөлугеболатынденелерсаналады.Мысалы,төмендекесіндіні,теңқабырғалыүшбұрышты,квадратты,кубтысәйкес2,4,8,өзұқсасэлементтергебөлутәсілікелтірілген.Суреттенфракталдыңқандаймасштабтабайқалғанынақарамастанбір-бірінеұқсас,бірдейтүргеиеекендігібілінеді.Бірақ,қосымшаешинформацияалмай,біртіндепкішірейіпнемесеүлкейіпотыратынөзұқсасөркеш-өркешбұлттардыңсыртқыпішінініңөлшемдерінбағалаумүмкінемес.Себебі,бұлкездеэлементтерсаныөтекөпжәнеоларбірсыдырғыорналаспайды.Бұлүшінарнайыөлшемділікұғымыенгізілуітиіс.

Жалпыөлшемділікұғымыкеңістіктегінүктеніңорнынанықтауғамүмкіндікберетін,еңазтәуелсізкоординаталарсанынанықтаументығызбайланысты.Физикадабұлгеометриялықобьектінібейнелеугемүмкіндікберетінтәуелсізайнымалыларсанымен–параметрлікөлшемділікпенсәйкескеледі.Евклидкеңістігіндегікөлемдіанықтауғакеректібұндайайнымалылардысаныүшкетең(x,y,z),жазықтықтыңауданынөлшеугеоныңекеуі(x,y)болса,алсызықүшінбіркоординатаxболсадажеткілікті.Нүктеніңөлшемділігінөлгетең.Осыжағынанкеңістікүшөлшемді,жазықтықекіөлшемді,алсызықбірөлшемдідепайтылады,яғни,параметрлікөлшемділіктіңмәндерібүтінсандар0,1,2,3.

Өлшемділіктіңекіншітүрінетопологиялықөлшемділікdжатады.Топологиялықөлшемділіктіңанықтамасыбылайберіледі:кез–келгенжиынныңтопологиялықөлшемділігіоныекі,өзарабайланыссызбөліктергеажырататынқиманыңөлшемділігінебірдіқосқанғатең.Түзудіекібайланыссызкескіндергебөлуоныңбірнүктесіналыптастауарқылыжүзегеасырылады.Алшектінүктелержиыныныңөлшемділігінөлгетеңболғандықтан,сызықбірөлшемді,яғни Жазықтықекіөлшемді,себебі,оныекігебөлудіөлшемді,екігетең,яғни, Демек,топологиялықөлшемділіктерде бүтінсандар.

Бірақ,табиғаттакездесетінкейбірнысандардыөлшеуүшін,бұлөлшемділіктержеткіліксізболыпшықты.Себебі,адамныңсезіммүшелерініңқабылдаушегінәртүрлісезімталқұралдар(микроскоптар,телескоптаржәнет.б.)арқылыбасқадеңгейгеауыстыруғаболады,бірақбарлықмасштабтыбірмезгілдеқадағалаужәненысандардыңөлшемдерініңәртүрлімасштабтақандайқатынастардаболатынынтағайындауқиын.Информациялыққордыңмолаюыменғылыми-техникалықпрогрессбұлқиындықтыжеңугемүмкіндікберді.

АлғашреткүрделінысандардыөлшеудіағылшынфизигіЛ.Ричардсонжүзегеасырды.Олфракталдыққұрылымдардыңбәрінеортақмаңыздыерекшеліктерініңбірі–олардыңаддитивтіеместігін,яғни,өлшенетіншама(ұзындық,аудан,көлем,масса,заряд,жәнет.б.)мәндерініңкеңістіктежүргізілгенөлшеулердіңдәлдігінетәуелділігінпайдаланды.Мысалы,асакүрделі,шым–шытырықброундықбөлшектіңтраекториясыныңұзындығыL,өлшеубірлігіне (масштабына)байланысты.Масштабкішірейгенсайынөлшенгенобьектініңұзындығыартабереді.[54]

Л.РичардсонБританияаралыныңәртүрлімасштабтатүсірілгенкарталарыналып,оныңАжәнеСнүктелерініңарасынқосатынжағалаусызығыныңұзындығынанықтауүшінадымы -ғатеңашаменөлшеулержүргізіледі.(2.3–сурет).АнүктесіненСнүктесінедейінжүріпөткендегіашаадымының 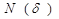санынбілуарқылыЛ.Ричардсонөлшенетінжағалаусызығыныңұзындығынмынаөрнекпенанықталады.

(2.2)

Бұлкезде масштабтыңішінекіретінкішіиілулер,ойыстармендөңестересептелмейтінібелгілі.Л.Ричардсонөлшеумасштабынкеішірейтіп,өлшеулердіқайталады.Ендібұрынғыкөптегениілулер,дөңестересептелгендіктен,өлшенгенұзындықбіршамаөсті.Сөйтіполашаныңадымынүнемікішірейтіпотыружағалаусызығыныңұзаруынаәкелетіншексізөзгертулеренгізугемүмкіндікберетінінбайқады.Сонымен,айыруқабілеттілігінарттыру,яғни,өлшеумасштабынкемітуәркездекүрделісызықтардыңұзаруынаәкеледі.

2.3сурет-Теңізжағалауыныңфрагменті.

Фракталдықнысандардыөлшеудіңтағыбіртәсіл-өлшенетіннысандардыөлшеудінемесеоныңфрагментін,қабырғаларыныңұзындығы -ғатең,квадратұяшықтарданқұралғанторларменжабу.Бұлкездедеөлшенетінфракталдықнысандытүгелжабатынұяшықтарсаны 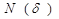анықталады.

Тәжірибелер,жағалаусызығыныңфрагментінжабатын,квадратұяшықтарыныңсаны,жуықшамаменсолқашықтықтытүгелөтетінашаадымыныңсанынатеңболатынынкөрсетті.Егержағалаусызығытұрақты ұзындыққаиеболса,ондаоныжабатынквадратұяшықтарыныңсаныөлшеумасштабынакеріпропорционал,ал(2.2)өрнекпенесептелетінжағалаусызығыныңұзындығы, кішірейгенсайын,тұрақты -геұмтылареді.Әрине,бұләдіспенөлшеукезіндеде кішірейгенгеартатындығыбайқалады.

Сонымен,Л.Ричардсонөлшеумасштабыкемігенсайын,фракталдықобьектініңжағалаусызығыныңөлшемідәрежелікзаңменөсетінінтағайындады.

, (2.3)

Мұндағы -өлшенетінобьектініңбастапқыжәнесоңғынүктелерінқосатынтүзудіңұзындығы, -өлшемсізшама.

БұлөрнекРичардсонзаңыдепаталады.Дәрежеліккөрсеткіш оңмәнгеиеболуытиіс.Жағалаусызығыныңұзындығынторменөлшеутәсіліндеде, өлшеумасштабыныңкемуітордытүзетінквадратұяшықтардыңсанынкөбейтетінболғандықтанРичардсонзаңыорындалады.

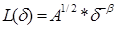, (2.4)

бұлжердеА–қабырғаларыныңұзындығы квадраттыңауданы.Өтекішімасштабтарда"жағалаусызығы"ұғымыныңмәніжоғалады.Алатомаралыққашықтықтарда"ашаадымы","квадратұяшық"ұғымдарыдаөзмәндерінжоятынытүсінікті.Себебі,бұлкездекванттықмеханиканыңзерттеуобылыстарынаенеміз.Бірақ,қалайдегенмен,Ричардсонзаңыкеңмасштабтыдиапазондаорындалатыныдәлелденді.Осыданжоғарыдатағайындалғанфизикалықзаңдылықтыңсипатынтүсінументүсіндірудіңматематикалыққұралыболуытиістігітуындайды.

Бұлқұралдытабуүшінкез–келгенфизикалықшаманыөлшеупроцесініңжалпысатыларықарастырылады,себебі,(2.3),(2.4)жаңадәрежелікзаңдарөлшеунәтижелерінесүйеніптағайындалған.Біз,обьектініңсанақжүйелерініңөзгерстерінебайланыссызтұрақтысипаттамаларын,яғни,инварианттысипаттамаларынқарастырамыз.Обектініңинварианттысипаттамаларыныңаддитивті(обьектініңсипаттамасыонықосындысынатең)жәнескалярлыболатыныбелгілі.

Жиындартеориясындаинвариантты,аддитивтіжәнескалярлықасиеттергеиесипаттамаларөлшемдепаталады.Класикалықфизикадаобьектініңөлшеміретіндеұзындықаудан,көлем,заряд,масса,олардыңбайқалуықтималдығыжәнет.б.жатады.

Математиктербіркелкіемескүрделіобьектілердібейнелеуүшінбөлшектік(Хаусдорф–Безикович)өлшемділігінқолданады.[55]Бұлөлшемділіктіанықтаудакеңістіктегінүктелердіңарақашықтығы,олардыңтаралузаңдылығынегізгірольатқарады.Осынүктелержиыныныңөлшемділігінтағайындауүшінөлшемұғымыенгізілген.

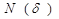Өлшенетіншаманытүгелжабатынкесінділердің,квадраттардың,кубтардыңсанынбілуобьектініңөлшемінанықтауғамүмкіндікбереді.Мысалы,қисықсызықтыңұзындығы,онытүгелжабатын,масштабты түзукесінділердің санынбілуарқылыанықталады(2.4-сурет).

2.4сурет–Ұзындықты,аудандыжәнекөлемдіөлшеуәдістері

Кәдімгітегісқисықүшін ,Алоныңұзындығы,шеккекөшуарқылы,мынаформуламенанықталады:

. (2.5)

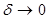ұмтылғадаөлшемLасимтоталытүрдеқисықтыңұзындығынатеңеледіжәне өлшеумасштабынатәуелсіз.

Нүктелержиынынажазықтықтысәйкестендіріпкөругеболады.Мысалы,қисықтытүгелдейжабатынквадраттардыңсанынбілуарқылыоныңауданынтауыпкөрейік.Бұлкездеөлшемаудан.Егеросықисықтыжабатынквадраттыңсаны 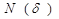,аләрквадраттыңауданы -қатеңболса,қисықтыңауданымынағантең:

.

Бұнда болса .Яғни,қисықтыңауданынөлгетең.Дәлосысияқтыетіп,қисықтыңкөлемдікөлшемінтексеругеболады.Бірақ,сызықтыңкөлеміболмайтынытүсінікті:

,

яғни , .

Ендібеттітүзетіннүктелержиынынқарастырайықжәнеоныңөлшеміретіндеұзындықалынсын.Бұлкезде 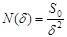,албеттіңұзындығы

(2.6)

Беттіңөлшеміретіндекөлемдіалыпкөрелік.Бұлкездеонытүгелжабатынкішікубтардыңкөлемініңқосындысымынағантең:

,

яғни 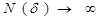, ,беттіңкөлемінөлгетеңеледі.Демек,ұзындықпенаудандыөлшеу(2.5)және(2.6)формулалармынатүрдежазылады:

, (2.7)

мұндағы {L,S,V}-өлшемнің(ұзындық,аудан,көлемжәнет.б.)жалпыбелгісі,алd–топологиялықөлшемділік.Нүкте,аудан,көлемдерүшінd=0,1,2,3.(1.6)формуланыфракталдықөлшемгеқолдануүшінолмынатүрдежазылады:

, (2.8)

бұлжерде -тұрақтышамалар,D–фракталдықөлшемділік.теңдеуденекіжағындалогарифмдеумынадайөрнекалуғамүмкіндікбереді:

немесе

(2.9)

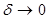,яғни,шеккекөшкенде,бұлөрнектіңоңжағындағыекіншімүше

Оданфракталдықөлшемділікмынатүрдеанықталады

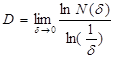(2.10)

БұлөрнекХаусдорфформуласыдепаталады.(2.10)өрнектіқолданубарысында, -ұяшықтыңөлшемі,ал -обьектініңөзұқсастығынқамтамасызететінеңазұяшықтарсаныекеніескерілуітиіс.

Date: 2016-05-25; view: 622; Нарушение авторских прав