
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оценка эксперта__
|
|
Задание 18 (=20 в 2015)
Самые общие инструкции по оцениванию выполнения заданий с развёрнутым ответом содержатся в критериях оценивания.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек  и/или и/или 
| |
| При всех значениях a верно найдено количество решений системы в одном из двух случаев, возникающих при раскрытии модуля | |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически или графически) ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задание 18(=20) - не только первое из двух сложных, четырёхбалльных заданий, но по факту – и самое сложное из них. Одновременное наличие системы уравнений, параметра и модуля (летом) сделало это задание наименее решаемым из всего набора заданий КИМ. Структура критериев оценивания выполнения этого задания, на самом деле, напоминает структуру критериев для задания 17(=19). Построение адекватной геометрической или алгебраической модели позволяет выставить 1 балл из четырех. Существенное продвижение (быть может, не до конца) в выбранной модели даёт 2 балла. Продвижение, при котором имеются минимальные неточности или описки позволяет выставить 3 балла.
Типичной границей между 1 баллом и «не пустой» работой на 0 баллов явилось верное нахождение уравнений двух окружностей без верного нахождения их точек пересечения. Здесь верно найдены «дуги окружностей», но неверно – их расположение. По критериям в таких случаях следует выставлять 0 баллов.
Слабо работающим оказался критерий на 2 балла. По факту, 2 балла следовало выставлять в случае успешного перехода к касательным в точке пересечения.
ВАРИАНТ 1
| 20 |
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений

имеет ровно два решения.
Решение.

|
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
1) Если  , то получаем уравнение
, то получаем уравнение
 ;
;
 ;
;
 .
.
Полученное уравнение задаёт окружность с центром в точке 
и радиусом  .
.
2) Если  , то получаем уравнение
, то получаем уравнение
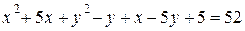 ;
;  ;
; 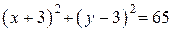 .
.
Полученное уравнение задаёт окружность с центром в точке 
и радиусом  .
.
Полученные окружности пересекаются в двух точках  и
и  , лежащих на прямой
, лежащих на прямой  , поэтому в первом случае получаем дугу
, поэтому в первом случае получаем дугу  с концами в точках
с концами в точках  и
и  , во втором — дугу
, во втором — дугу  с концами в тех же точках (см. рис.).
с концами в тех же точках (см. рис.).
Рассмотрим второе уравнение системы. Оно задаёт прямую  , которая проходит через точку
, которая проходит через точку  и угловой коэффициент которой равен
и угловой коэффициент которой равен 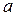 .
.
При  прямая
прямая  проходит через точки
проходит через точки  и
и  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При  прямая
прямая  перпендикулярна прямой
перпендикулярна прямой  , угловой коэффициент которой равен
, угловой коэффициент которой равен  , значит, прямая
, значит, прямая  касается дуги
касается дуги 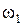 в точке
в точке  и пересекает дугу
и пересекает дугу  в двух точках (одна из которых — точка
в двух точках (одна из которых — точка  ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При  прямая
прямая  перпендикулярна прямой
перпендикулярна прямой  , угловой коэффициент которой равен
, угловой коэффициент которой равен  , значит, прямая
, значит, прямая  касается дуги
касается дуги  в точке
в точке 
и пересекает дугу 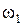 в двух точках (одна из которых — точка
в двух точках (одна из которых — точка  ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При  или
или  прямая
прямая  пересекает каждую из дуг
пересекает каждую из дуг 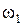 и
и  в точке
в точке 
и ещё в одной точке, отличной от точки  , то есть исходная система имеет три решения.
, то есть исходная система имеет три решения.
При  прямая
прямая  пересекает дугу
пересекает дугу  в двух точках (одна из которых — точка
в двух точках (одна из которых — точка  ) и не пересекает дугу
) и не пересекает дугу 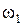 в точках, отличных от точки
в точках, отличных от точки  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При  прямая
прямая  пересекает дугу
пересекает дугу 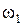 в двух точках (одна из которых — точка
в двух точках (одна из которых — точка  ) и не пересекает дугу
) и не пересекает дугу  в точках, отличных от точки
в точках, отличных от точки  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
Значит, исходная система имеет ровно два решения при  . Ответ:
. Ответ:  .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек  и/или и/или 
| |
| При всех значениях a верно найдено количество решений системы в одном из двух случаев, возникающих при раскрытии модуля | |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически или графически) ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
ВАРИАНТ 2
| 20 |
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений
 имеет ровно два решения.
имеет ровно два решения.
Ответ:.
Пример 1.


Комментарий. Очень редкий случай «дохождения» до касательных. К сожалению, ошибка с вычислением левого конца отрезка не позволяет поставить 3 балла.
Оценка: 2 балла
Пример 2.

Комментарий. Судя по рисунку, точка (2;1) у автора НЕ лежит на нужной прямой. Ответ не обоснован никак и неизвестно, как получен.
Оценка: 0 баллов.
Пример 3.


Комментарий. Сложный случай. Автор нащупал верную идею про угол между касательными. Но есть явно неверное утверждение про их симметричность и неверное нахождение тангенса угла их наклона. Поэтому до 2 баллов, к сожалению, не дотягивает.
Оценка: 1 балл
Date: 2016-05-25; view: 476; Нарушение авторских прав