
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Для расчета электростатических полей
|
|
В случае электростатических полей, обладающих симметрией (плоской, осевой или сферической), теорема Гаусса позволяет достаточно просто получить выражение для определения модуля вектора  . Для этого достаточно теорему применять по следующей схеме:
. Для этого достаточно теорему применять по следующей схеме:
- в каждой точке поля из симметрии поставленной задачи определяют направление вектора  ;
;
- выбирают замкнутую поверхность (поверхность интегрирования) и определяют поток вектора  через неё. Выбранная поверхность должна отражать симметрию поля, и внутри неё должен находиться заряд (или часть заряда);
через неё. Выбранная поверхность должна отражать симметрию поля, и внутри неё должен находиться заряд (или часть заряда);
- определяют величину заряда, заключенного внутри поверхности;
- применяют теорему Гаусса (1. 21).
1.12.1. Поле равномерно заряженной
бесконечно протяженной плоскости
Так как плоскость заряжена равномерно, то во всех её точках поверхностная плотность зарядов  одинакова, поэтому поле такой плоскости однородно. Линии вектора
одинакова, поэтому поле такой плоскости однородно. Линии вектора  перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны (рис.1.11,а).
перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны (рис.1.11,а).
 а)
а)
|

б) |
Рис.1.11. Поле равномерно заряженной бесконечно протяженной плоскости:
а – к применению теоремы Гаусса; б – график зависимости Е от r
Выбираем замкнутую цилиндрическую поверхность, основания которой параллельны заряженной плоскости, а ось перпендикулярна ей. В таком случае линии вектора напряженности пересекают только два основания поверхности, поток через которые согласно (1.18) может быть определен:
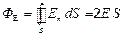 ,
,
где S – площадь основания поверхности.
Применяем теорему Гаусса (1.21):
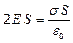 , откуда
, откуда  . (1.25)
. (1.25)
На рис.1.11,б приведен график зависимости модуля вектора  в зависимости от
в зависимости от  , где
, где  - расстояние от плоскости до точки, в которой определяется значение
- расстояние от плоскости до точки, в которой определяется значение 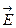 .
.
Используя связь между напряженностью и потенциалом поля (1.7), можно определить разность потенциалов между двумя точками поля, расположенными на расстоянии  и
и 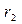 от плоскости (см.рис.1.11,а)
от плоскости (см.рис.1.11,а)
 .
.
В заключение отметим, что реальная плоскость может быть принята за бесконечно протяженную при условии, что её размеры значительно больше расстояния от неё до точек, в которых определяется напряженность.
1.12.2. Поле плоского конденсатора
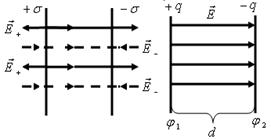
Используя выражение (1.26) и принцип суперпозиции полей, можно определить напряженность поля плоского конденсатора (рис.1.12). Из построения силовых линий (см.рис.1.12,а) следует, что поле вне пластин отсутствует (слева и справа от пластин линии напряженности 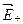 и
и 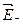 направлены навстречу друг другу), а внутри конденсатора:
направлены навстречу друг другу), а внутри конденсатора:
 ,
,
где  – модуль заряда пластины; S – площадь пластины.
– модуль заряда пластины; S – площадь пластины.
 а) б)
а) б)
|
| Рис.1.12. Поле плоского конденсатора, создаваемое каждой из пластин конденсатора в отдельности (а) и результирующее поле между обкладками (б) |
Разность потенциалов ( ) (иначе напряжение U) между пластинами определим согласно (1.8):
) (иначе напряжение U) между пластинами определим согласно (1.8):
 , (1.27)
, (1.27)
где 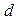 - расстояние между пластинами.
- расстояние между пластинами.
Приведенные расчеты справедливы при условии, что расстояние между пластинами значительно меньше размеров пластин.
1.12.3. Поле равномерно заряженной
бесконечно длинной прямой нити
Для равномерно заряженной нити во всех её точках линейная плотность заряда  будет одинаковой, поэтому поле имеет осевую симметрию: линии вектора
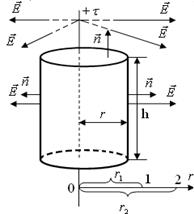
будет одинаковой, поэтому поле имеет осевую симметрию: линии вектора  представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис.1.13,а). На одинаковых расстояниях от нити, т.е. на цилиндрической поверхности модуль
представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис.1.13,а). На одинаковых расстояниях от нити, т.е. на цилиндрической поверхности модуль  будет одинаковым.
будет одинаковым.
|

| ||
| а) б) Рис.1.13. Поле бесконечной равномерно заряженной нити |
Поверхность интегрирования выбирают цилиндрическую, ось которой совпадает с нитью. Поток вектора  через основания цилиндра равен нулю (линии напряженности их не пересекают), поэтому остается поток только через боковую поверхность и согласно (1.18) получим:
через основания цилиндра равен нулю (линии напряженности их не пересекают), поэтому остается поток только через боковую поверхность и согласно (1.18) получим:
 ,
,
где r – радиус цилиндра (расстояние от нити до точки, где определяется напряженность); h – высота цилиндрической поверхности.
Определяем заряд внутри цилиндрической поверхности:
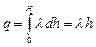 .
.
Применяем теорему Гаусса (1.21):
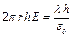 , откуда
, откуда  .
.
На (рис.1.13,б) приведен график зависимости модуля вектора  от расстояния от нити до точки, в которой он определяется.
от расстояния от нити до точки, в которой он определяется.
Используя связь между потенциалом и напряженностью поля (1.7), можно определить разность потенциалов между двумя точками поля, находящимися на расстояниях  и
и 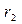 от нити (см.рис.1.13,а):
от нити (см.рис.1.13,а):
 .
.
В заключение отметим, что приведенные выводы справедливы для нити конечной длины при условии, что её длина значительно больше расстояния от нити до точки, в которой определяется напряженность.
1.12.4. Поле равномерно заряженной сферической поверхности радиуса R и заряда q
Поле сферической поверхности обладает центральной симметрией – линии вектора  представляют собой прямые, выходящие из поверхности, перпендикулярные к ней (рис.1.14). Вне сферы на одинаковых расстояниях от ее центра модуль вектора
представляют собой прямые, выходящие из поверхности, перпендикулярные к ней (рис.1.14). Вне сферы на одинаковых расстояниях от ее центра модуль вектора  будет одинаковым.
будет одинаковым.
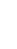  
| 
| ||||||||

| |||||||||
| а) б) Рис.1.14. К определению характеристик поля заряженной сферической поверхности: а – равномерно заряженная сферическая поверхность; б – зависимости Е (r) и φ (r) |
Поверхность интегрирования выбираем в виде сферы, центр которой совпадает с центром заряженной сферы (точка О) и имеющей радиус r. Поток вектора 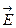 через эту сферу (1.18):
через эту сферу (1.18):
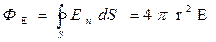 ;
;  .
.
Если  , внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле и по теореме Гаусса (1.21):
, внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле и по теореме Гаусса (1.21):
 , откуда
, откуда  ,
,

Если 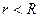 , то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует.
, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует.
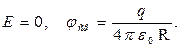
- Если  справедливы следующие равенства:
справедливы следующие равенства:
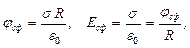
где 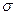 - поверхностная плотность заряда, согласно (1.24):
- поверхностная плотность заряда, согласно (1.24):

 Рис.1.15. Поле сферического конденсатора
Рис.1.15. Поле сферического конденсатора
|
 Таким образом, можно сделать вывод, что внутри сферы поле отсутствует, а за её пределами оно совпадает с полем точечного заряда q, помещенного в центр сферы.
Таким образом, можно сделать вывод, что внутри сферы поле отсутствует, а за её пределами оно совпадает с полем точечного заряда q, помещенного в центр сферы.
Графики зависимости 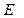 и
и  от
от  , где
, где  - расстояние от центра сферы до точки, в которой определяются напряженность и потенциал поля, приведены на рис.1.14,б.
- расстояние от центра сферы до точки, в которой определяются напряженность и потенциал поля, приведены на рис.1.14,б.
С помощью принципа суперпозиции легко определить поле двух сферических поверхностей, имеющих общий центр (точка O, рис.1.15), которые заряжены одинаковыми по величине, но различными по знаку зарядами. Такая система называется сферическим конденсатором. В общей внутренней части меньшей и большей сфер поле отсутствует. В зазоре между поверхностями напряженность поля Е определяется по формуле:
 ,
,
где 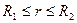 .
.
Разность потенциалов между сферами определяется по формуле (1.8):
 .
.
Поле сферического конденсатора в отличие от поля плоского является неоднородным.
1.12.5. Поле объемно-заряженного шара
с равномерной плотностью заряда
Пусть шар радиуса R заряжен с постоянной объемной плотностью  . Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат, что и в случае заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса
. Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат, что и в случае заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса  (
(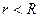 ) заключает в себе заряд равный:
) заключает в себе заряд равный:  . Поэтому теорему Гаусса (1.21) для такой поверхности запишем следующим образом:
. Поэтому теорему Гаусса (1.21) для такой поверхности запишем следующим образом:
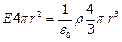 .
.
Отсюда, заменив  , получим
, получим

Таким образом, внутри шара напряженность поля растет линейно с расстоянием  от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда. В центре шара
от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда. В центре шара  .
.
Date: 2016-05-18; view: 658; Нарушение авторских прав