В электростатическом поле. Теорема о циркуляции

вектора напряжённости электростатического поля

Предположим, что некоторый точечный заряд перемещается в поле неподвижного точечного заряда 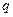из точки 1 в точку 2 (рис.1.8). На заряд действует сила, и, следовательно, совершается работа. Первоначально определим работу на малом перемещении :

или ,

где – проекция вектора силы на направление перемещения .

Следовательно, , но , где равно приращению модуля радиуса-вектора , поэтому . Так как заряды точечные, то

.

Работа, совершаемая при перемещении заряда из точки 1 в точку 2, определяется выражением:

(1.9)

или после интегрирования

. (1.10)

Из выражения (1.10) можно сделать следующие выводы:

– работа не зависит от формы траектории, по которой движется заряд q_0,, зависит от положения начальной 1 и конечной 2 точек перемещения. Силовые поля, удовлетворяющие этому условию, называют потенциальными, а силы, действующие в этих полях называют консервативными. Следовательно, электростатическое поле потенциально, а силы в этом поле консервативны;

– работа, совершаемая при перемещении заряда q₀ вдоль замкнутой траектории (r₁ = r₂), равна нулю.

Если силовые линии замкнуты, то такое поле называется вихревым. К таким полям относятся магнитное и возбуждаемое переменным магнитным – электрическое.

Работу, совершаемую при перемещении заряда в поле вдоль замкнутого контура, можно определить выражением:

, так как .

Согласно выражению (1.8) эта работа равна нулю и, следовательно,

. (1.11)

Выражение называют циркуляцией вектора напряжённости электростатического поля, а (1.11) теоремой о циркуляции .

Выражение (1.11) позволяет решать многие задачи, связанные с электростатическим полем.

Date: 2016-05-18; view: 622; Нарушение авторских прав