Эквипотенциальные поверхности

Для более наглядного графического изображения полей, кроме линий напряжённости, используют поверхности равного потенциала или эквипотенциальные поверхности. Как следует из названия, эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция x, y, z, то уравнение эквипотенциальной поверхности имеет вид:

.

Линии напряжённости поля перпендикулярны эквипотенциальным поверхностям.

Докажем это утверждение.

Пусть линия и силовая линия составляют некоторый угол 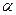(рис.1.5).

Переместим из точки 1 в точку 2 вдоль линии пробный заряд . При этом силы поля совершают работу:

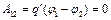. (1.5)

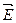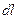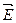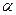То есть работа перемещения пробного заряда вдоль эквипотенциальной поверхности равна нулю. Эту же работу можно определить и другим способом – как произведение заряда на модуль напряженности поля, действующего на пробный заряд, на величину перемещения и на косинус угла между вектором и вектором перемещения , т.е. косинус угла (см.рис.1.5):

.

Величина работы не зависит от способа её подсчёта, согласно (1.5) она равна нулю. Отсюда вытекает, что и, соответственно, , что и требовалось доказать.

Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Условились, однако, проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была бы всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряжённости поля. Действительно, чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности.

На рис.1.6,а показаны эквипотенциальные поверхности (точнее, их пересечения с плоскостью чертежа) для поля точечного заряда. В соответствии с характером изменения эквипотенциальные поверхности при приближении к заряду становятся гуще. На рис.1.6,б изображены эквипотенциальные поверхности и линии напряжённости для поля диполя. Из рис.1.6 видно, что при одновременном использовании эквипотенциальных поверхностей и линий напряжённости картина поля получается особенно наглядной.

Для однородного поля эквипотенциальные поверхности, очевидно, представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению напряжённости поля.

1.8. Связь между напряжённостью поля и потенциалом

(градиент потенциала)

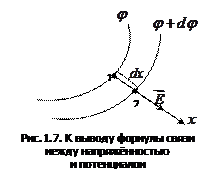Пусть имеется произвольное электростатическое поле. В этом поле проведём две эквипотенциальные поверхности таким образом, что они отличаются одна от другой потенциалом на величину dφ (рис. 1.7)

Вектор напряжённости направлен по нормали к поверхности . Направление нормали совпадает с направлением оси x. Ось x, проведённая из точки 1, пересекает поверхность 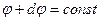в точке 2.

Отрезок dx представляет собой кратчайшее расстояние между точками 1 и 2. Работа, совершаемая при перемещении заряда 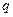вдоль этого отрезка:

.

С другой стороны, эту же работу можно записать как:

.

Приравнивая эти два выражения, получаем:

, (1.6)

где символ частной производной подчёркивает, что дифференцирование производиться только по x. Повторив аналогичные рассуждения для осей y и z, можем найти вектор :

, (1.7)

где – единичные векторы координатных осей x, y, z.

Вектор, определяемый выражением (1.7), называется градиентом скаляра φ. Для него наряду с обозначением применяется также обозначение . («набла») означает символический вектор, называемый оператором Гамильтона

.

Следовательно, из определения градиента можно записать:

,

т.е. напряжённость поля 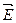равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости 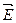поля направлен в сторону убывания потенциала.

По формуле (1.7) можно найти проекцию вектора 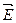на выбранное направление в пространстве, например, на ось x:

или , (1.8)

где () − разность потенциалов между точками 1 и 2, расположенными на оси x.

Date: 2016-05-18; view: 975; Нарушение авторских прав