Поток вектора напряженности. Теорема Гаусса

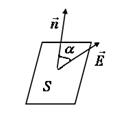
Предположим, что имеется однородное электростатическое поле, в котором расположен плоский контур площадью S (рис.1.9). Под потоком вектора 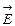, пронизывающим площадку S, понимают произведение напряженности поля на площадь контура и на косинус угла 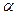между вектором напряженности и нормалью к контуру. Для однородного поля:

.

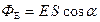Поток может принимать положительное значение, если угол 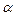острый, и отрицательное, если угол 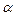тупой. При 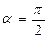поток равен нулю. Учитывая, что 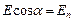, где 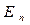- проекция вектора напряженности на направление нормали, 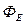можно определить выражением:

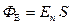. (1.17)

Если поле неоднородное, а контур не плоский, то для определения потока необходимо контур мысленно разделить на малые элементы площади. В пределах каждой такой площади поле можно принимать за однородное, а сам элемент площади за плоский. Поток, связанный с одним из элементов, 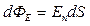, а со всей поверхностью:

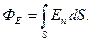(1.18)

Выражение (1.18) является наиболее общим определением потока вектора напряженности поля. Кроме того, поток может быть определен как общее число силовых линий, пронизывающих поверхность.

Определим поток через сферическую поверхность 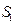, в центре которой расположен точечный заряд 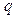(рис.1.10).

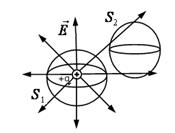
Рис.1.9. К определению потока вектора напряженности	Рис.1.10. К выводу теоремы Гаусса

В силу центральной симметрии напряженность поля в каждой точке поверхности одинакова по модулю и может быть определена по формуле (1.4), тогда выражение (1.17), учитывая, что 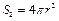, примет вид:

.

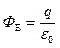Можно сделать выводы:

- поток вектора не зависит от радиуса сферы;

- при перемещении заряда внутри сферы поток вектора не изменяется, так как общее число линий напряженности поля, пересекающих данную поверхность, остается прежним. По этой же причине при замене сферической поверхности на любую произвольную замкнутую поверхность поток не меняется;

- если поверхность 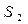(см.рис.1.10) не охватывает заряд, то поток вектора будет равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий выходящих.

Если внутри замкнутой поверхности расположено N зарядов, то поток 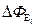от произвольного заряда :

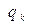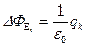, (1.19),

где 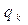– значение k -го заряда.

Просуммировав значение потоков в формуле (1.18) получим:

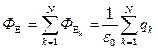. (1.20)

Так как суммарный поток 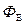через замкнутую поверхность определяется выражением (1.17), то, приравняв правые части формул (1.17) и (1.20),получим:

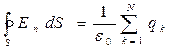. (1.21)

Полученное выражение (1.21) называется теоремой Гаусса. Согласно этой теореме поток вектора напряженности электростатического поля в вакууме через замкнутую поверхность любой формы равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленных на .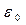

Применение теоремы Гаусса для произвольного распределения зарядов может столкнуться с математическими трудностями, однако в случаях, обладающих симметрией, многие задачи решаются просто.

При решении подобных задач используют понятие объемной плотности заряда 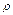, определяемого по формуле:

.

При равномерном распределении заряда 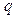по объему :

.

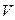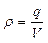Кроме того, используют понятия 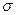поверхностной и линейной 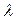плотностей зарядов, определяемых соответственно по формулам:

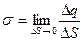; (1.22)

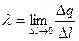. (1.23)

При равномерном распределении зарядов:

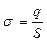; (1.24)

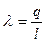. (1.25)

Зная плотности, можно определить величину зарядов, заключенных внутри поверхностей.

Теорема Гаусса позволяет решать две задачи: 1) определение распределения напряженности поля при известном распределении зарядов и 2) определение распределения зарядов по заданному распределению напряженности.

Date: 2016-05-18; view: 719; Нарушение авторских прав