Линейная регрессионная модель

Любую систему можно представить в виде «черного ящика» (рис.2.2.1):

Обозначения на рис.2.2.1:

x_n − входные параметры;

y_m − выходные параметры;

ε _k − воздействие трудно учитываемых факторов (возмущений).

Поставим задачу: изучить зависимость между входными X и выходными Y параметрами в виде математической модели. В качестве математической модели могут выступать различные уравнения, системы уравнений, дифференциальные уравнения и их системы. Если поставлена задача, о выявлении зависимости в виде некоторой функции то она является задачей регрессионного анализа, а полученные зависимости линиями регрессии.

Пусть произведено n опытов, в которых наблюдались изменения как случайной величины X, так и Y. В результате эксперимента получено n пар наблюдений (x_i; y_i) (рис. 2.2.2).

Нас интересует функция, которая бы приблизительно описывала зависимость между величинами. По опытным данным можно построить несколько линий регрессии. Возникает вопрос, какая линия наилучшим образом воспроизводит зависимость между X и Y. Для решения подобных задач обычно применяется метод наименьших квадратов, при котором требование наилучшего согласования кривой Y=f(X) и экспериментальных точек сводится к тому, что сумма квадратов отклонений эксnериментальных данных y_i от линии Y=f (x_i) должна быть минимальной:

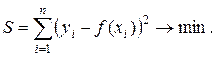
На основании метода наименьших квадратов получаем линейную регрессионную модель:

(2.2.4)

Данное уравнение также называют выборочным линейным уравнением регрессии.

Проводя аналогичные исследования, можно построить уравнение зависимости X от Y:

(2.2.5)

Пример 3. Вычислить выборочный коэффициент корреляции и построить линейные регрессионные модели по данным корреляционной таблицы 2.2.2:

Таблица 2.2.2

X Y	12,5	22,5	32,5	42,5	52,5	62,5
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-
	-	-	-

 

Решение. Для определения выборочных характеристик подсчитаем частоты появления значений случайных величин X и Y и представим их отдельными таблицами (табл. 2.2.3) и (табл. 2.2.4).

Таблица 2.2.3

X	12,5	22,5	32,5	42,5	52,5	62,5

 

Найдем выборочное среднее для X по формуле (2.1.2):

Выборочная дисперсия и выборочное среднее квадратичное отклонение вычисляются по формулам (2.1.4) и (2.1.6):

Аналогичные вычисления выполним и для величины Y.

Таблица 2.2.4

Y

 

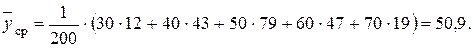
Выборочный корреляционный момент определяется по формуле (2.2.3). Предварительно вычислим сумму:

Тогда выборочный коэффициент корреляции найдем по формуле (2.2.4):

Следует отметить, что близость выборочного коэффициента корреляции по модулю к единице является серьезным аргументом в пользу выбора линейной регрессионной модели.

Подставляем найденные выборочные характеристики в уравнение линейной регрессии Y на X (2.2.4):

Таким же образом находим уравнение линейной регрессии X на Y:

Если построить обе прямые линии регрессии на одном графике (рис.2.2.3), то они пересекутся в точке с координатами .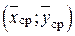

Выборочный коэффициент корреляции по модулю приближается к единице, поэтому угол между прямыми линиями – острый.

 

Date: 2016-05-18; view: 558; Нарушение авторских прав