Доверительный интервал для оценки математического ожидания и дисперсии нормального распределения при неизвестном σ

При малом числе наблюдений точечная оценка в значительной степени случайна, и замена истинного значения параметра на оценку может привести к серьезным ошибкам.

Чтобы дать представление о точности и надежности оценки в математической статистике используют так называемые доверительные интервалы и доверительную вероятность.

Пусть найденная по данным выборки величина ã служит оценкой неизвестного параметра а. Оценка ã определяет параметр а, тем точнее, чем меньше | а − ã |, т.е. чем меньше величина εв неравенстве | а − ã |<ε, ε > 0.

Так как оценка ã − случайная величина, то и разность | а − ã | − случайная величина. Поэтому неравенство | а − ã |<ε, при заданном ε, можетвыполняться только с некоторой вероятностью.

Доверительной вероятностью (надежностью) оценки ã параметра а называется вероятность β, с которой оценивается неравенство | а − ã |<ε.

Доверительную вероятность β назначают достаточно большой (0,9; 0,95; 0,99) такой, чтобы событие с вероятностью β можно было считать практически достоверным. Затем находят такое значение ε, для которого

Р (| а − ã |<ε)= β.

В этом случае диапазон возможных значений ошибки, возникающей при замене параметра а на оценку ã, будет ±ε. Большие по абсолютной величине ошибки будут появляться только с малой вероятностью α = 1−β, которую называют вероятностью риска или уровнем значимости.

Неравенство | а − ã |<εможно записать в виде

− ε < а − ã < εили ã − ε < а < ã + ε.

Доверительным интервалом называется интервал (ã − ε; ã + ε ), который покрывает неизвестный параметр а с заданной надежностью β. Доверительный интервал также можно рассматривать как интервал значений параметра а, совместимых с опытными данными и не противоречащих им.

Доверительный интервал для математического ожидания имеет вид:

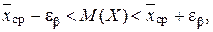(2.2.1)

где и −значение статистики Стьюдента для числа степеней свободы k= n- 1и доверительной вероятности β, которые находятся по таблице 4 приложения.

Для построения доверительного интервала для дисперсии используют распределение . Вид этого закона распределения очень сложен, поэтому значения распределения представлены в таблице 3 приложения. Они зависят от числа степеней свободы и от доверительной вероятности.

Доверительный интервал для дисперсии имеет вид

(2.2.2)

Пример 1. Произведено 20 опытов над случайной величиной X, распределенной по нормальному закону. Требуется построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности β=0,8, если получены оценки математического ожидания и дисперсии:

S ² = 0,064.

Решение. По таблице 4 приложения находим значение распределения Стьюдента для числа степеней свободы k= n- 1 = 20-1=19и доверительной вероятности β = 0,8:

Тогда

Доверительный интервал для математического ожидания принимает вид

10,78− 0,751 < M(Х) < 10,78 + 0,751,

10,029 < M(Х) < 11,531.

Если доверительная вероятность β=0,8, то уровень значимости α=0,2. По таблице 3 приложения найдем значения распределения :

Доверительный интервал для дисперсии:

0,0447 < D(X) < 0,1039.

Date: 2016-05-18; view: 1268; Нарушение авторских прав