
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выборочный коэффициент корреляции
|
|
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от другой случайной величины Х.
Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической зависимостью, либо быть независимыми.
Строгая функциональная зависимость реализуется редко, так как обе случайные величины или одна из них подвержены действию случайных факторов, в этом случае возникает статистическая зависимость.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае статистическую зависимость называют корреляционной.
Для оценки связи между случайными величинами обычно используется выборочный коэффициент корреляции.
Введем в рассмотрение выборочный корреляционный момент:
 (2.2.3)
(2.2.3)
Выборочный коэффициент корреляции представляет собой отношение:
 (2.2.4)
(2.2.4)
где Sx и Sy − выборочные средние квадратичные отклонения случайных величин X и Y соответственно.
Выборочный коэффициент корреляции измеряет силу (тесноту) линейной связи между величинами X и Y.
Пример 2. Найти выборочный коэффициент корреляции по данным корреляционной таблицы 2.2.1.
Таблица 2.2.1
| X Y |
| |||
| − | ||||

| n= 16 |
Решение. Найдем оценки числовых параметров распределения.
Выборочные средние вычисляем по формуле (2.1.2):


Несмещенные выборочные дисперсии:

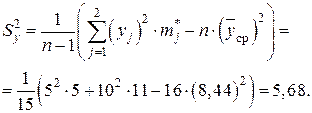
Выборочные средние квадратичные отклонения:


Выборочный корреляционный момент:



Таким образом, выборочный коэффициент корреляции равен:

Выборочный коэффициент корреляции приближается к нулю, поэтому зависимость между случайными величинами не является линейной, она может быть выражена какой-либо иной зависимостью.
Date: 2016-05-18; view: 994; Нарушение авторских прав