
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выборка и способы ее представления
|
|
Всю совокупность экспериментальных данных будем называть генеральной совокупностью.
Однако, получение экспериментальных данных достаточно трудоемкий, дорогой процесс, а в некоторых случаях и просто невозможный. Поэтому из всей генеральной совокупности приходится выбирать только определенную часть объектов, которую называют выборочной совокупностью или выборкой объема n.
Предположим, что над случайной величиной Х производится ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина Х принимает определенное значение: x 1, x 2 ,…, xn. Совокупность этих значений рассматривается как простая выборка.
Наблюдаемое значение xi называют вариантой, а их последовательность, записанную в возрастающем порядке, - вариационным рядом. Для каждой варианты можно указать частоту ее появления, которую обозначают 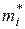 . Также может быть найдена относительная частота появления определенной варианты, как отношение частоты к объему выборки:
. Также может быть найдена относительная частота появления определенной варианты, как отношение частоты к объему выборки:
 .
.
Сумма всех относительных частот  должна быть равна единице.
должна быть равна единице.
Не трудно заметить, что относительная частота имеет смысл статистическойвероятности.
Статистическим распределением или статистическим рядом называют соответствие вариант и их частот (табл.2.1.1) или относительных частот (табл.2.1.2).
Таблица 2.1.1
| X | x 1 | x 2 | ... | xk |

| 
| 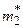
| ... | 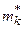
|
Или
Таблица 2.1.2
| X | x 1 | x 2 | ... | x k |
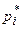
| 
| 
| ... | 
|
Пример 1. Записать в виде вариационного ряда выборку 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4. Представить статистическое распределение выборки.
Решение. Объем выборки n =15. Упорядочив элементы выборки по величине, получим вариационный ряд 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7, 10, 10. Различными в заданной выборке являются элементы х 1=2, х 2=3, х 3=4, х 4=5, х 5=7, х 6=10; их частоты соответственно равны  =3,
=3,  =1,
=1, 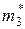 =2,
=2,  =3,
=3,  =4,
=4, 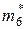 =2. Следовательно, статистическое распределение исходной выборки можно записать в виде следующей таблицы:
=2. Следовательно, статистическое распределение исходной выборки можно записать в виде следующей таблицы:
Таблица 2.1.3
| xi | ||||||

|
Для контроля правильности записи находим 
Для каждого значения варианты можно найти также относительные частоты. В этом случае таблица для статистического ряда принимает следующий вид (табл. 2.1.4):
Таблица 2.1.4
| Х | ||||||
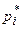
| 
| 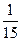
| 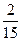
| 
| 
| 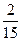
|
При большом числе наблюдений статистический ряд перестает быть удобной формой записи статистического материала – он становится громоздким и мало наглядным. Для придания ему большей компактности и наглядности строится так называемый интервальный статистический ряд. В этом случае весь диапазон наблюдаемых значений Х разделяется на интервалы и подсчитывается количество значений  , приходящееся на каждый интервал (табл. 2.1.5).
, приходящееся на каждый интервал (табл. 2.1.5).
Таблица 2.1.5
| Границы интервалов | x 1; x 2 | x 2; x 3 | ... | xk; xk+ 1 |
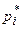
| 
| 
| ... | 
|
Длину интервала – h –проще выбирать одинаковой. Практика показывает, что число интервалов рационально выбирать порядка 7-20. Для нахождения длины интервала можно воспользоваться формулой:
 (2.1.1)
(2.1.1)
Если в результате вычисления по формуле (2.1.1) длина интервала получится дробным числом, от выбирают либо близкое целое число, либо близкую простую дробью.
Пример 2. Представить выборку в виде интервального статистического ряда:
38 60 41 51 33 42 45 21 53 60
68 52 47 46 49 49 14 57 54 59
77 47 28 48 58 32 42 58 61 30
61 35 47 72 41 45 44 55 30 40
67 65 39 48 43 60 54 42 59 50.
Решение. Объем выборки n= 50. Наибольшая варианта – 77, наименьшая – 14. Найдем длину интервала по формуле (2.1.1):
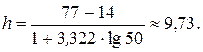
Выбираем длину интервала 9. Интервальный статистический ряд принимает вид (табл. 2.1.6).
Таблица 2.1.6
| Границы интервалов | [14;23) | [23;32) | [32;41) | [41;50) | [50;59) | [59;68) | [68;77] |

| |||||||
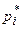
| 0,04 | 0,06 | 0,12 | 0,34 | 0,2 | 0,18 | 0,06 |
Date: 2016-05-18; view: 986; Нарушение авторских прав