Числовые характеристики непрерывных случайных величин

Так же как для дискретной случайной величины, для непрерывной случайной величины вычисляются числовые характеристики.

Математическим ожиданием случайной величины Х называется ее среднее значение, вычисляемое по формуле: – для непрерывной случайной величины.

Мода. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум

Медианой M _e случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.

Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Дисnерсия для непрерывной случайной величины определяется по формуле: .

Более простая формула для вычисления дисперсии имеет вид: D [ X ]= M [ X ²]-(M [ X ])²,

где M [ X ²]

Средним квадратичным отклонением случайной величины Х называется корень квадратный из дисперсии .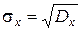

Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х^k:

Для непрерывной случайной величины:

.

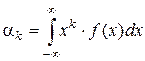Начальный момент первого порядка равен математическому ожиданию.

Центральным моментом порядка k случайной величины Х называется математическое ожидание величины :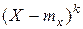

.

Для непрерывной случайной величины:

.

Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Отношение центрального момента третьего порядка к среднему квадратичному отклонению в третьей степени называется коэффициентом асимметрии:

.

Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом:

.

Пример 4. Случайная величина подчинена закону распределения с плотностью:

Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до .

Решение. Построим график плотности распределения (рис. 1.2.3):

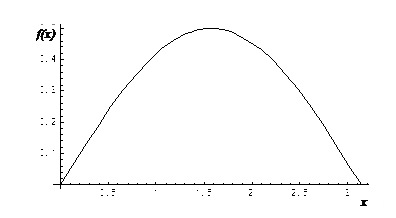
Рис. 1.2.3

Для нахождения коэффициента а воспользуемся свойством:

.

Пример.5. Задана непрерывная случайная величина х своей функцией распределения f(x):

Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал . определить математическое ожидание и дисперсию случайной величины Х.

Найдем коэффициент А.

Найдем функцию распределения:

1) На участке :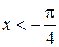

2) На участке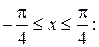

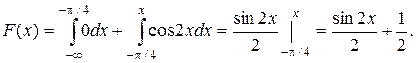
3) На участке

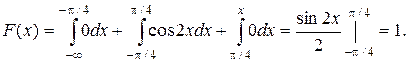
Таким образом:

Построим график плотности распределения (рис.1.2.4) и интегральной функции распределения (рис. 1.2.5).

Найдем вероятность попадания случайной величины в интервал .

Рис. 1.2.4

Рис. 1.2.5

Ту же самую вероятность можно искать и другим способом:

Определим математическое ожидание:

Для нахождения дисперсии вычислим

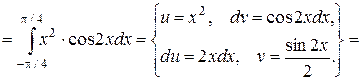
Date: 2016-05-18; view: 712; Нарушение авторских прав