
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числовые характеристики дискретной случайной величины
|
|
Закон распределения полностью характеризует случайную величину. Но он не всегда известен. Существуют некоторые числовые характеристики, описывающие случайную величину суммарно. Прежде всего, это характеристики положения: математическое ожидание, медиана, мода; характеристики рассеяния: дисперсия, среднее квадратичное отклонение.
Математическим ожиданием случайной величины X называется ее среднее значение, вычисляемое по формуле: 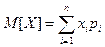 – для дискретной случайной величины. В случае, когда М [ Х ]надо обозначить одной буквой, будем писать М [ Х ]= mx или Мх.
– для дискретной случайной величины. В случае, когда М [ Х ]надо обозначить одной буквой, будем писать М [ Х ]= mx или Мх.
Модой М 0 дискретной случайной величины называется ее наиболее вероятное значение.
Медианой M e случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.
 .
.
Для дискретной случайной величины обычно медиана не определяется.
Рассмотрим свойства математического ожидания дискретной случайной величины.
1. Математическое ожидание постоянной величины равно ей самой, т.е. M [ C ] = C;
2. Постоянный множитель можно выносить за знак математического ожидания, т.е. M [ C × X ] = C × M [ X ];
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е.
М [ X × Y ]= M [ X ] ×M [ Y ];
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, т.е.
М [ X + Y ] = M [ X ] + M [ Y ].
Свойства 3 и 4 обобщаются на случай нескольких случайных величин.
Знание математического ожидания случайной величины еще полностью не характеризует эту случайную величину. По этому числу нельзя еще судить ни о возможных значениях случайной величины, ни о том, как эти значения рассеяны вокруг математического ожидания.
Пример 3. Заданы две случайные величины X и Y (табл.1.2.7 и табл.1.2.8)
Таблица 1.2.7
| X | -0,01 | 0,01 |
| P | 0,5 | 0,5 |
Таблица 1.2.8
| Y | -100 | |
| P | 0,5 | 0,5 |
Найти их математические ожидания.
Решение.
M [ X ]= -0,01×0,5+ 0,01×0,5=0;
M [ Y ]=-100×0,5+100×0,5=0.
Как видно из примера, случайные величины имеют разные возможные значения, но одинаковые математические ожидания, причем случайная величина X имеет возможные значения близкие к M [ X ], а случайная величина Y - далекие. Здесь налицо малое и большое рассеяние возможных значений вокруг среднего. Для оценки величины рассеяния используют новую числовую характеристику - дисперсию дискретной случайной величины.
Дисnерсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D [ X ]= M [ X - M [ X ]]2.
Дисперсию ДСВ вычисляют по формуле:  .
.
Пример 4. Найти дисперсию случайной величины X,заданную следующим законом распределения (табл. 1.2.9):
Таблица 1.2.9
| X | |||
| P | 0,3 | 0,5 | 0,2 |
Решение.
M [ X ]= 1×0,3+ 2×0,5+ 5×0,2=2,3;
(x 1 – M [ X ])2=(1-2,3)2=1,69;
(x 2 – M [ X ])2=(2-2,3)2=0,09;
(x 3– M [ X ])2=(5-2,3)2=7,29;
D [ X ]=1,69×0,3+0,09×0,5+7,29×0,2=2,01.
Более простая формула для вычисления дисперсии имеет вид:
D [ X ]= M [ X 2]-(M [ X ])2.
Поясним ее применение на предыдущем примере. Для ее использования необходимо составить закон распределения случайной величины X 2 (табл. 1.2.10).
Таблица 1.2.10
| X 2 | |||
| P | 0,3 | 0,5 | 0,2 |
M [ X 2]= 1×0,3 + 4×0,5 + 25×0,2 = 7,3;
D [ X ]=7,3-(2,3)2=2,01.
Использование этой формулы существенно сокращает число арифметических действий.
Дисперсия D [ X ]кратко обозначается Dx. Рассмотрим свойства дисперсии дискретной случайной величины.
1. Дисперсия постоянной величины равна нулю, т.е. D [ C ] = 0;
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е. D [ C×X ] = C 2× D [ X ];
3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий, т.е. D [ X + Y ] = D [ X ] + D [ Y ].
4. Дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины, т.е. сдвиг возможных значений случайной величины не изменяет рассеяния:
D [ C + X ] = D [ X ].
5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е. D [ X - Y ] = D [ X ] + D [ Y ].
Недостатком дисперсии является то, что она имеет размерность, равную квадрату размерности случайной величины. Если это существенно в эксперименте, то используют другую числовую характеристику, среднее квадратичное отклонение.
Средним квадратичным отклонением случайной величины Х называется корень квадратный из дисперсии 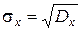 .
.
Кроме характеристик положения и рассеяния существует ряд других числовых характеристик распределения, например, моменты.
Date: 2016-05-18; view: 803; Нарушение авторских прав