
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации к практическому занятию. 1. Студент должен уметь для каждой серии параллельных опытов определять среднее арифметическое значение по формуле:
|
|
1. Студент должен уметь для каждой серии параллельных опытов определять среднее арифметическое значение по формуле:
 , (2.5.1)
, (2.5.1)
где  номер серии;
номер серии;
 номер опыта в серии;
номер опыта в серии;
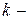 число параллельных опытов.
число параллельных опытов.
2. Рассчитать оценки дисперсий для всех серий опытов, пользуясь формулой:
 . (2.5.2)
. (2.5.2)
С каждой из этих оценок дисперсий связано число степеней свободы:
 . (2.5.3)
. (2.5.3)
3. Рассчитать средневзвешенную оценку дисперсии по формуле:
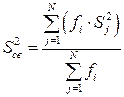 . (2.5.4)
. (2.5.4)
4. Гипотеза о равенстве нескольких выборочных дисперсий (для нескольких серий измерений), т. е. их однородности, характеризует воспроизводимость (т. е. степень близости друг друга) результатов измерений, полученных в разных условия.
Критерий Бартлетта используется для проверки гипотезы о воспроизводимости опытов в тех случаях, когда имеются результаты нескольких серий параллельных опытов, однако число опытов в этих сериях разное. Расчетное значение коэффициента Бартлетта определяется по формуле:
 . (2.5.5)
. (2.5.5)
где 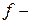 суммарное число степеней свободы:
суммарное число степеней свободы:
 ; (2.5.6)
; (2.5.6)
С – вспомогательный коэффициент:
 . (2.5.7)
. (2.5.7)
5. Проверить гипотезу о воспроизводимости результатов неравноточных измерений с помощью критерия Бартлетта:
 . (2.5.8)
. (2.5.8)
Значение B сравнивается со значением 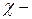 критерия для уровня значимости q и числа степеней свободы
критерия для уровня значимости q и числа степеней свободы 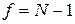 (таблица 2.5.1). Если условие (2.5.8) выполнено, то принимается гипотеза о воспроизводимости опытов. В качестве оценки дисперсии воспроизводимости принимается величина
(таблица 2.5.1). Если условие (2.5.8) выполнено, то принимается гипотеза о воспроизводимости опытов. В качестве оценки дисперсии воспроизводимости принимается величина  , с которой связано число степеней свободы f, определяемое по формуле (2.5.4).
, с которой связано число степеней свободы f, определяемое по формуле (2.5.4).
Таблица 2.5.1 – Значения критерия 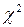

| 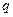
| ||||
| 0,01 | 0,02 | 0,05 | 0,10 | 0,20 | |
| 0,000 | 0,001 | 0,004 | 0,016 | 0,064 | |
| 0,020 | 0,040 | 0,103 | 0,211 | 0,446 | |
| 0,115 | 0,185 | 0,352 | 0,584 | 1,005 | |
| 0,297 | 0,429 | 0,711 | 1,064 | 1,649 | |
| 0,554 | 0,752 | 1,145 | 1,610 | 2,34 | |
| 0,872 | 1,134 | 1,645 | 2,20 | 3,07 | |
| 1,239 | 1,564 | 2,17 | 2,83 | 3,82 | |
| 1,646 | 2,03 | 2,73 | 3,49 | 4,59 | |
| 2,09 | 2,53 | 3,32 | 4,17 | 5,38 | |
| 2,56 | 3,06 | 3,94 | 4,86 | 6,18 |
Рассмотрим пример проверки гипотезы. Результаты этого эксперимента приведены в таблице 2.5.2. В качестве функции отклика было принято напряжение в электрической цепи 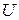 , (В). Как видно из таблицы, число параллельных опытов в трех сериях различное. Следует также отметить, что для проверки гипотезы с помощью критерия Бартлетта число опытов в серии должно быть не менее трех.
, (В). Как видно из таблицы, число параллельных опытов в трех сериях различное. Следует также отметить, что для проверки гипотезы с помощью критерия Бартлетта число опытов в серии должно быть не менее трех.
Таблица 2.5.2 – Экспериментальные и расчетные данные для проверки гипотезы о воспроизводимости опытов
| Номер серии опытов | Напряжение 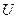 , В , В
| 
| 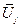
| 
| |||
| 1 опыт | 2 опыт | 3 опыт | 4 опыт | ||||
| 85,2 | 83,8 | 86,4 | - | 85,1 | 2,70 | ||
| 92,7 | 90,5 | 89,8 | 93,4 | 91,6 | 2,97 | ||
| 76,4 | 74,3 | 77,9 | - | 76,2 | 3,27 |
1. Для каждой серии опытов вычисляем среднее арифметическое значение выхода целевого продукта по формуле 2.5.1:
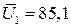 В;
В;  В;
В;  В.
В.
2. Рассчитываем оценки дисперсий для всех серий параллельных опытов по формуле (2.5.2):
 ;
;  ;
; 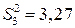 .
.
3. С этими оценками связаны числа степеней свободы, вычисленные по формуле (2.5.3):
 ;
;  ;
;  .
.
4. Средневзвешенную оценку дисперсии рассчитываем по формуле (2.5.4):
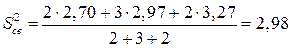 .
.
5. Вычислим вспомогательный коэффициент по формуле (2.5.7):
 .
.
6. Рассчитаем значение коэффициента Бартлетта по формуле (2.5.5):
 .
.
7. В таблице 2.5.1 находим значение критерия 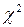 для уровня значимости
для уровня значимости  и числа степеней свободы
и числа степеней свободы 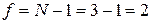 . Оно равно 0,103. Тогда:
. Оно равно 0,103. Тогда: 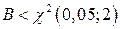 .
.
Следовательно, можно принять гипотезу о воспроизводимости опытов.
Date: 2016-05-18; view: 478; Нарушение авторских прав