Методические рекомендации к практическому занятию. 1. Студент должен уметь определять среднее арифметическое значение функции отклика для каждой серии параллельных опытов:

1. Студент должен уметь определять среднее арифметическое значение функции отклика для каждой серии параллельных опытов:

, (2.4.1)

где номер серии;

номер опыта в серии;

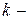число параллельных опытов.

2. Рассчитать оценки дисперсий для всех серий опытов, пользуясь формулой:

. (2.4.2)

3. Для проверки гипотезы о принадлежности двух выборочных дисперсий одной генеральной совокупности (их однородности), а, следовательно, и равноточности серий измерений (показатель воспроизводимости опытов в эксперименте) используется критерий Кочрена

Для проверки гипотезы с помощью критерия Кочрена необходимы результаты нескольких серий параллельных опытов. В каждой из них количество опытов должно быть одинаково. Обычно число серий не велико – . Количество опытов в серии также может быть небольшим – . Расчетное значение критерия Кочрена представляет собой отношение наибольшей из оценок дисперсий к сумме всех найденных оценок дисперсий:

. (2.4.3)

4. Найти критическое значение критерия Кочрена G в таблице 2.4.1.

Гипотезу о воспроизводимости опытов принимают, если выполнено условие:

. (2.4.4)

В этом случае оценки дисперсий всех серий проведенных опытов считаются однородными, т. е. принадлежащими к одной генеральной совокупности.

Таблица 2.4.1 – Критические точки распределения Кочрена при уровне значимости

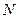
	0,9985	0,9750	0,9392	0,9057	0,8772	0,8534	0,8332
	0,9669	0,8709	0,7977	0,7457	0,7071	0,6771	0,6530
	0,9065	0,7679	0,6841	0,6287	0,5895	0,5598	0,5365
	0,8412	0,6338	0,5981	0,5440	0,5063	0,4783	0,4564
	0,7808	0,6161	0,5321	0,4803	0,4447	0,4184	0,3980
	0,7271	0,5612	0,4800	0,4307	0,3974	0,3726	0,3535
	0,6798	0,5157	0,4377	0,3910	0,3595	0,3362	0,3185
	0,6385	0,4775	0,4027	0,3584	0,3286	0,3067	0,2901
	0,6020	0,4450	0,3733	0,3311	0,3029	0,2823	0,2666
	0,5410	0,3924	0,3624	0,2880	0,2624	0,2439	0,2299

5. На основании однородных оценок дисперсий вычислить величину, называемую оценкой дисперсией воспроизводимости опытов, по формуле:

. (2.4.5)

С нею связано число степеней свободы, вычисляемое по формуле:

. (2.4.6)

Оценка дисперсии воспроизводимости используется при анализе результатов активного эксперимента для проверки статистических гипотез о значимости коэффициентов регрессии и об адекватности уравнения регрессии.

Рассмотрим пример проверки гипотезы с помощью критерия Кочрена. Допустим, что для проверки гипотезы о воспроизводимости опытов выполнен эксперимент, состоящий из трех серий по два параллельных опыта

в каждой. Результаты этого эксперимента приведены в таблице 2.4.2. В качестве функции отклика было принято напряжение в электрической цепи 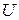, (В). Будем считать, что условия проведения различных серий опытов отличаются друг от друга.

1. Вычислим средние значения напряжения в электрической цепи в каждой серии опытов по формуле (2.4.1):

В; В; В.

Результаты вычислений внесем в таблицу 2.4.2.

Таблица 2.4.2 – Экспериментальные и расчетные данные для проверки гипотезы о воспроизводимости опытов

Номер серии опыта	В
Результат 1-го опыта	Результат 2-го опыта
	35,0	36,0	35,5	0,50
	39,3	38,1	38,7	0,72
	31,8	33,4	32,6	1,28

2. Рассчитаем оценки дисперсий для каждой серии опытов по формуле (2.4.2):

; ; .

Вычисленные значения поместим в таблицу 2.4.2.

3. С каждой из этих оценок дисперсий связано число степеней свободы, вычисленное по формуле (2.4.6):

.

4. Вычислим расчетное значение критерия Кочрена по формуле (2.4.3):

.

5. Соответствующее критическое значение критерия Кочрена берем из таблицы 2.4.1. При уровне значимости , числе серий опытов и числе степеней свободы находим значение .

Очевидно, что , следовательно, можно принять гипотезу о том, что опыты воспроизводимы. В этом случае оценки дисперсий, содержащиеся в таблице 2.4.2, можно считать однородными.

6. Вычислим оценку дисперсии воспроизводимости по формуле (2.4.5):

.

С ней связано число степеней свободы, найденное по формуле (2.4.6):

.

Date: 2016-05-18; view: 225; Нарушение авторских прав