Определение теоретического закона распределения производственных погрешностей

Подбор теоретической кривой, соответствующей полученной эмпирической кривой, называется выравниваем статистических рядов. Задача выравнивания заключается в том, чтобы подобрать теоретическую кривую распределения, наиболее точно описывающую полученное эмпирическое распределение.

Подбор теоретической кривой осуществляется на основании математического анализа опытных данных выборочной совокупности или из предложений, что каждому теоретическому закону распределения соответствуют вполне определенные условия функционирования технологических операций. При этом графики эмпирических зависимостей сравниваются с образцами известных кривых. Для определения того, насколько правильно функция описывает опытное распределение, используются различные критерии согласия.

Рис. 5. Гистограмма (1), эмпирическая (2) и теоретическая (3) кривые плотности распределения вероятности

После выбора подходящей теоретической кривой производится ее построение. Рассмотрим построение теоретической кривой нормального закона распределения как наиболее характерного и распространенного при оценке точности технологических операций.

Теоретическая кривая плотности вероятности определяется выражением вида

где 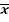, , S - числовые значения параметров эмпирического распределения, найденные в предыдущем разделе.

Для облегчения расчетов по формуле (2.8) пронормируем распределение: перенесем начало координат в центр группирования и выразим x в долях S.

Введя для нормированного аргумента обозначение Z, получим

,

где - значение признака качества в середине j-го интервала. При этом длина интервала .

Определив по формуле (2.9) значения для каждого интервала, найдем с помощью табл. П.2 (см. Приложение) соответствующие им значения плотностей 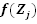. Полученные данные заносятся в табл. 2 и используются для построения теоретической кривой плотности распределения вероятности.

Теоретическая кривая плотности распределения вероятности выполняется на одном графике с эмпирической кривой (рис. 5).

После построения теоретической кривой с помощью статистического критерия согласия проверяется гипотеза о соответствии этой кривой эмпирическому распределению.

Таблица 2

Номер интервала	Середина интервала	Значение теорети-ческой плотности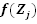
1
j
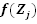
L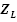

2.5. Проверка гипотезы о соответствии эмпирического и теоретического распределения с помощью критерия (Пирсона).

Для объективной оценки степени соответствия выбранного теоретического распределения эмпирическому используются различные статистические критерии согласия. Сущность этих критериев сводится к тому, что выбирается некоторый ко­личественный показатель меры расхождения между выбранным теоретическим распределением и эмпирическим, Если такая мера расхождения (т.е. критерий) для рассматриваемого случая превосходит допустимый предел , то гипотеза отвергается; если , то гипотеза принимается.

В качестве меры расхождения обычно берут определенным образом выбранную функцию от разности между теоретической и эмпирической плотностями вероятности и либо разности между теоретической и эмпирической функцией распределения и .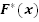

Рассмотрим применение одного из наиболее употребительных в технологии критериев – критерия (Пирсона).

Величина критерия определяется по формуле

,

где 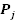- теоретическая вероятность нахождения в j –м интервале.

Величина характеризует меру расхождения между теоретическими 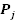и эмпирическими вероятностями распределения случайной величины x в каждом j -м интервале. Следовательно, есть также величина случайная.

Для расчета критерия по формуле (2.10) необходимо вычислить значения теоретических вероятностей 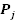для каждого j -го интервала, определяемые выражением вида

.

Данные для расчета критерия оформляются в виде табл. 3.

Таблица 3

Номер интервала	Теоретическая вероятность	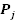Эмпирическая вероятность
1
j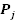
L

При использовании критерия количество частот в каждом j -м интервале должно быть не менее 5-ти. Если данное условие не выполняется, то необходимо объединить соседние интервалы. В результате этого число объединенных интервалов по сравнению с L уменьшается, и значения теоретических и эмпирических вероятностей для k -го объединенного интервала определяется суммой соответствующих вероятностей объединяемых интервалов. В процессе расчета суммирование ве­дется по , т.е.

.

Определив по данным табл. 3 экспериментальное значение , не­обходимо сравнить его с теоретическим , которое дано в табл. П. 3 (см. Приложение) в зависимости от числа степеней свободы r и равного

,

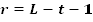где t - число параметров закона распределения (для нормального закона t=2).

По числу степеней свободы r в табл. П. 3 (см. Приложение) выбирается такое значение , при котором выполняется условие и определяется вероятность выполнения этого условия, т.е. 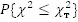. Для принятия выдвинутой гипотезы о соответствии теоретического закона должно соблюдаться соотношение

.

Если , то выдвинутая гипотеза отвергается и для имеющего эмпирического распределения подбирается другой теоретический закон.

Date: 2016-05-18; view: 685; Нарушение авторских прав