Определение эмпирического закона распределения производственных погрешностей

Определение эмпирической кривой плотности распределения вероятности производственных погрешностей исследуемой технологической операции производится с помощью больших и малых выборочных совокупностей (выборок). Выборка – совокупность элементов (деталей), которые выбираются из генеральной совокупности для получения достоверных сведений о всей совокупности. Число членов n, образующих выборку, составляет ее объем. Большой выборочной совокупностью считается выборка объемом , а малой - . От правильного определения объема выборки зависит объем исследований, сроки, в которые оно будет проведено, затраты, а также точность и достоверность результатов исследования.

Рис. 4. Кривые плотности распределения
вероятности с различными значениями эксцесса

Выборки по отношению ко времени их образования могут быть единовременными и мгновенными (текущими). Единовременной является выборка, которая отобрана из партии деталей после их изготовления. Для обеспечения представительности выборки все детали должны быть перемешаны между собой. Мгновенной является выбора, которая состоит из деталей, последовательно изготовленных за определенный промежуток времени на данном станке при данной настройке.

По мгновенной выборке объемом от 5 до 20 деталей, полученных в последовательности их обработки на одном станке, определяют влияние случайных факторов на качество изготовления деталей. По общей выборке, состоящей из 10 и более мгновенных выборок, взятых последовательно с одного станка за межнастроечный период или с момента установки нового инструмента до его замены, определяют раздельно влияние случайных и систематических факторов на качество изготовления деталей за межнастроечных период без учета погрешности настройки.

Совместное влияние случайных и систематических факторов, в том числе и погрешности настройки, на качество деталей, изготовленных на одном станке при одной или нескольких настройках, можно определить по большой единовременной выборке (объем от 50 до 200 деталей) случайно отобранных деталей.

Каждая деталь, входящая в выборку, измеряется с помощью универсально-измерительных приборов, цена деления измерительной шкалы которых должна удовлетворять условию [2]

,

где - допуск на размер деталей по чертежу, мм.

Результаты измерений деталей выборки в табл. П.1.

Для построения эмпирической кривой распределения все измеренные значения располагают в порядке возрастания или в порядке убывания и разбивают на ряд интервалов. От выбора числа интервалов зависит метод и объем вычислительных работ, а также степень наглядности опытных данных при построении графиков распределения. Рекомендуется [1] при объеме выборки 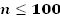определять число интервалов L по формуле

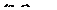
, (2.6)

а при объеме выборки - по формуле

. (2.7)

Числа интервалов, рассчитанных по формулам (2.6) и (2.7), приведены ниже

Ширина интервала H, т.е. разность между максимальными и минимальными 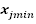значениями признака внутри j -го интервала определяется по формуле

,

где - размах выборки; , - максимальное и минимальное значения признака в выборке.

Определив величину и положение интервалов, необходимо подсчитать частоты или частости для каждого из них. Частота – это количество деталей, входящих в выборку, измеряемый признак качества которых попал в j -й интервал. Частость – отношение числа деталей, признак качества которых попал в j -й интервал? К объему всей выборки. Частость представляет собой эмпирическую вероятность попадания признака качества в j -й интервал, т.е. (знаком “*” будем обозначать все эмпирические характеристики в отличие от теоретических). Сумма эмпирических вероятностей (частостей) всех интервалов очевидно должна быть равна единице .

Полученные выше данные удобно представить в виде
табл. 1 и использовать для построения гистограммы, эмпирического закона распределения и расчета его основных характеристик (математического ожидания 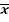, дисперсии , среднего квадратического отклонения S).

Таблица 1

Номер интервала	Интервал	Середина интервала	Частота	Частость	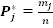Эмпирическая плотность распределения вероятности.
1
J
L

Числовые характеристики определяются по формулам (2.3), (2.4), (2.5).

Гистограмма строится следующим образом. По оси абсцисс откладываются интервалы и на каждом из них, как на основании, строятся прямоугольники, площади которых равны частостям соответствующих интервалов. Для построения гистограммы нужно частость каждого интервала разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине интервалов высоты прямоугольников пропорциональны частостям. Высота j -го прямоугольника представляет собой значение эмпирической плотности распределения вероятности признака качества в j -м интервале, т.е. . Для приведения к одинаковому масштабу кривых эмпирического и теоретического распределения при построении гистограммы необходимо пользоваться формулой , где - нормированная длина интервала, определяемая из выражения .

Гистограмма имеет вид, показанный на рис. 5. Площадь гистограммы равна . Из способа построения гистограммы следует, что она является аналогом эмпирической плотности распределения. При увеличении объема выборки и уменьшении длины интервалов гистограмма будет все более приближаться к кривой плотности распределения. На практике эмпирическая кривая плотности распределения проводится следующим образом. На верхней стороне каждого из построенных прямоугольников гистограммы отмечаются точками их середины. Соединяя получение точки кривой, получают график функции , представленный на рис. 5.

После построения эмпирического закона распределения и расчета его числовых параметров осуществляется подбор и построение теоретической кривой.

Date: 2016-05-18; view: 905; Нарушение авторских прав