Достаточные условия экстремума для функции двух переменных

Теорема: Если функция 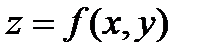имеет непрерывные частные производные до третьего порядка включительно, в окрестности точки 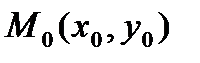и эта точкаявляется стационарной точкой.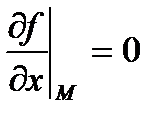 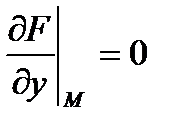, то в точке 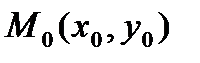существует локальный максимум, если:

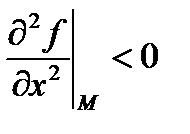
1) 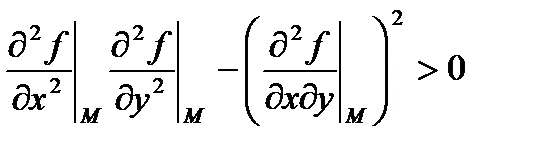В этом случае локальный максимум.

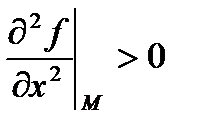
2) 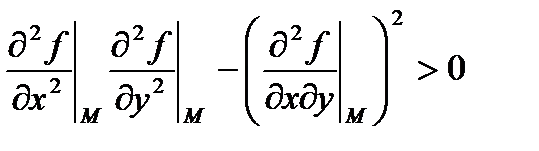локальный минимум.

3) 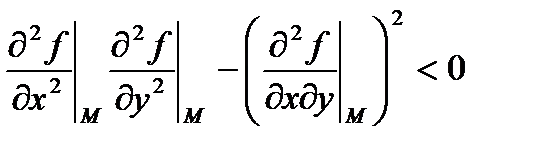локальный экстремум не существует.

4) 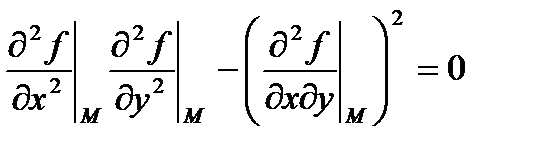возможны любые ситуации.

Доказательство: обозначим , ,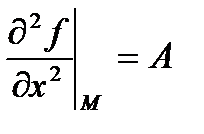

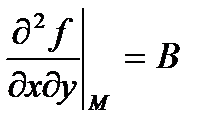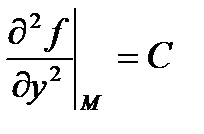
Тогда второй дифференциал в точке 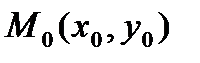: 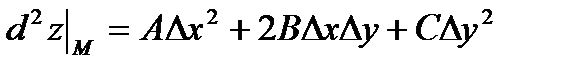При этом матрица квадратичной формы имеет вид: 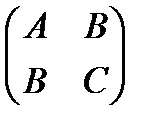. Характеристический многочлен квадратичной матрицы будет иметь вид: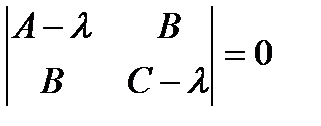

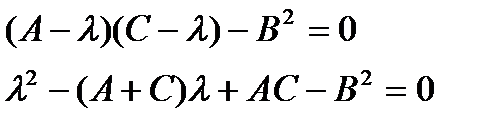
Согласно теореме Виета, произведение корней равно 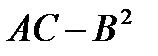, а сумма равна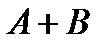

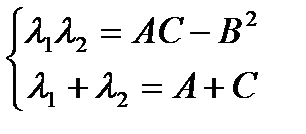
Таким образом, видим, чтобы квадратичная форма была знакоопределена необходимо, чтобы произведение собственных значений было положительным 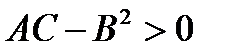. При этом

если сумма собственных значений отрицательна, то квадратичная форма отрицательно определенная, если сумма собственных значений положительна, то квадратичная форма положительно определённая. Преобразуем выражение стоящее в левой части равенства:

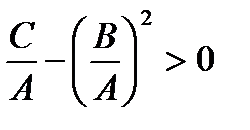; то есть 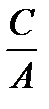- положительная величина.

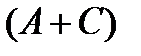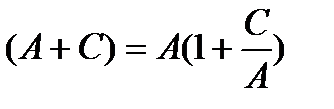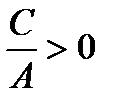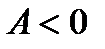Выражение можно представить в виде: , так как , то выражение в скобках положительно, знак собственных значений совпадает со знаком величины , то есть если , то в точке M локальный максимум (случай 1);

Если 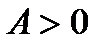то в точке M локальный минимум (случай 2).

Если 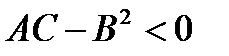, то собственное значение 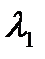и 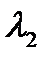имеют разный знак. В этом случае существует направление, для которого точка M является точкой максимума и существует направление, для которого точка M является точкой минимум, такую точку называют минимакс. Дадим геометрическую интерпретацию первых трёх случаев:

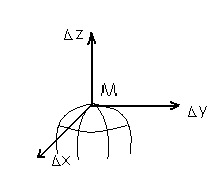1)

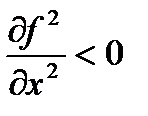
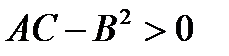
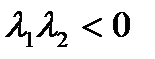
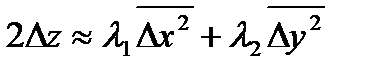
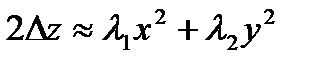
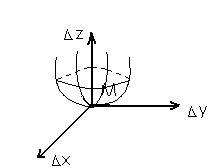2)

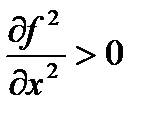
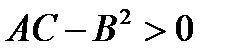
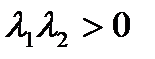
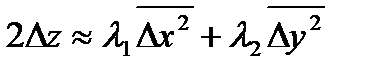
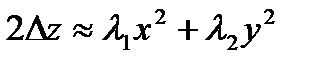
3)

,

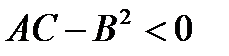
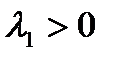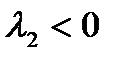
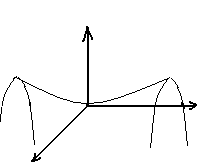
Если на наибольшее и наименьшее значения исследуется функция несколько переменных, в замкнутой ограниченной области, то согласно теореме Вейерштрасса, она достигает своих наименьших и наибольших значений.

Если наибольшее (наименьшее) значение достигается во внутренних точках, то эти точки

являются точками локального экстремума.

Таким образом, для нахождения наибольшего (наименьшего) значения нужно исследовать локальные точки экстремума и поведение функции на границе области.

Условный экстремум.

Пусть требуется найти экстремумы функции

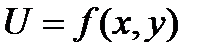, (1)

при условии, что переменные 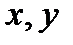связаны соотношением

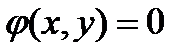(2).

Если возможно разрешить выражение (2) относительно одной из переменных, например, определить как функцию от , то подставим в выражение (1), получим задачу на экстремум функции одной переменной.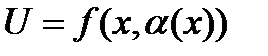

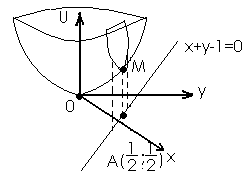
Пример: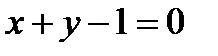

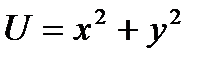
Из рисунка видим, что безусловный экстремум достигается в точке 0. Условный экстремум(экстремум функции), рассматриваемой на заданной прямой, достигается в точке A.

,

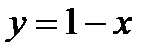
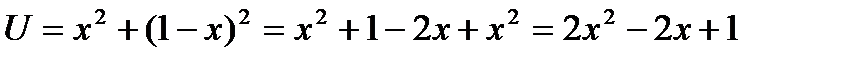
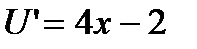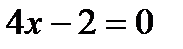
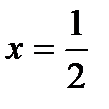
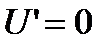
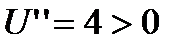. В этой точке 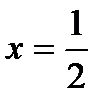существует локальный минимум .

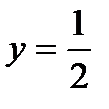Таким образом, M является точкой локального минимума, для значений удовлетворяющих прямой.

Рассмотрим метод, нахождения условного экстремума без разрешения условий связи (2). Найдём полную производную функции U, считая y функцией от x

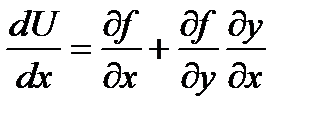, (3)

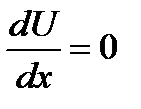C другой стороны производная функции 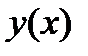определяется неявно соотношением (2).

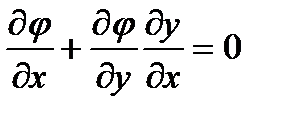(4)

Умножим выражение (4) на 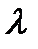и сложим с (3), получим

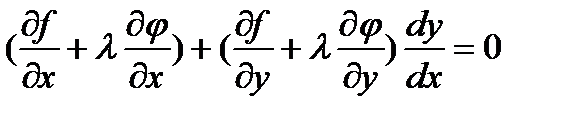(5)

Последнее условие выполняется в точках экстремума.

Подберём 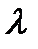так чтобы, вторая скобка обращалась в 0.

Из (5) получим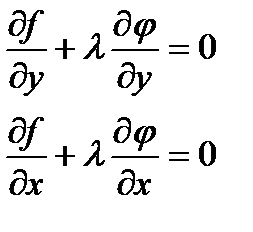

Присоединив к двум уравнениям выражение (2) получим систему (6), трёх уравнений с тремя неизвестными

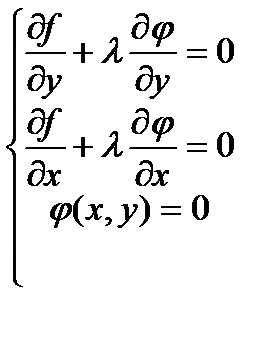(6)

Разрешив систему (6), найдём точки подозрительные на экстремум. Легко заметить, что (6) образована из первых производных, по 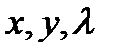от функции

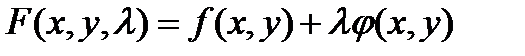(7)

(7)- функция Лагранжа, параметр 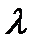называется множителем Лагранжа.

В случае функции n – переменных

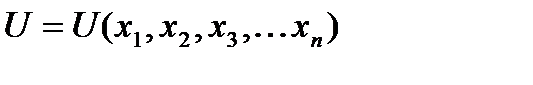и условии связи , где .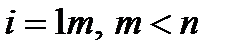

Функция Лагранжа

.

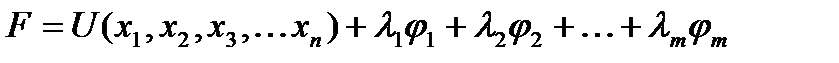Для нахождения точек условного экстремума выписывают систему 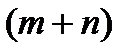- уравнений, и 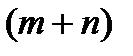- неизвестных.

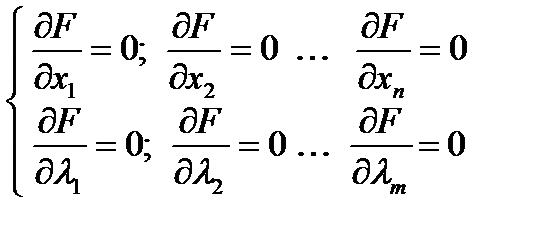
Вопрос о наличии у подозрительных точек экстремума решается с помощью дополнительного исследования.

Пример: 8.207

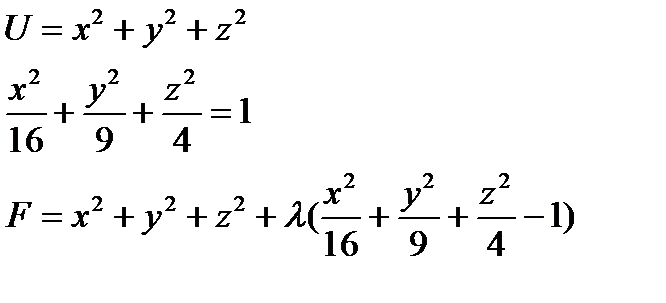
Находим первую производную по

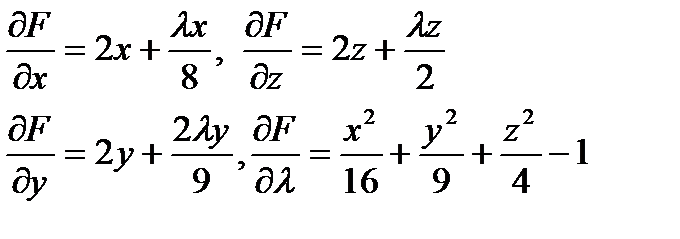
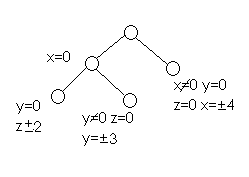
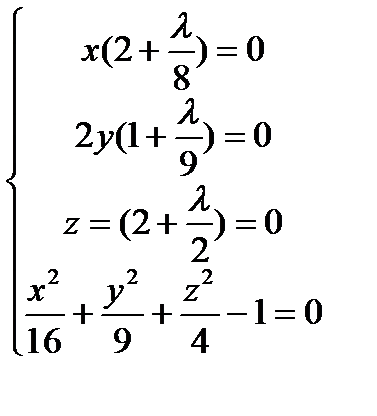
Серии точек 1)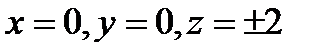

2)

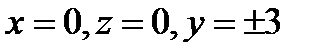
3)

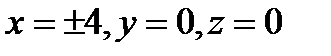
Для исследования экстремума в этих точках необходимо рассмотреть 3 случая:

1) когда условие связи определяет функцию как функцию от переменных х, у;

2) условие связи определяет у как ;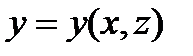

3) когда ;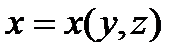

Найдем частные производные от 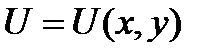, рассматривая z как функцию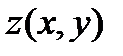

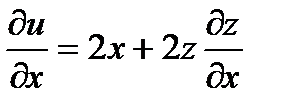
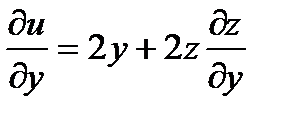; величины 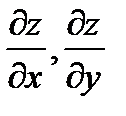определим из уравнений связи;

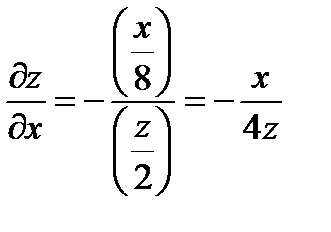
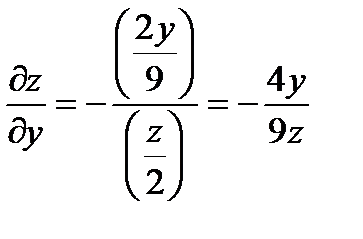
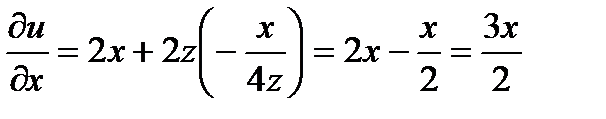
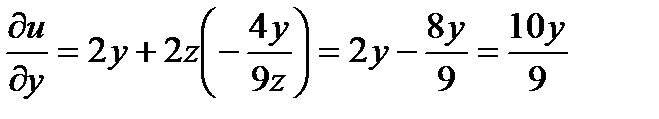
Видим, что найденные производные обращаются в 0, когда 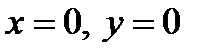в точках первой серии. Вычислим вторые производные в этих точках.

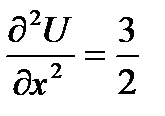
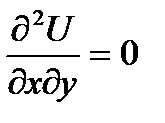
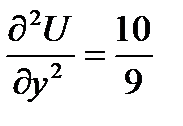
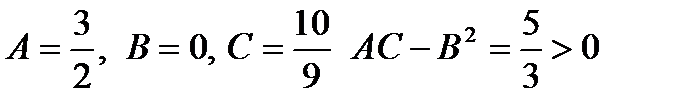, А>0 min

Пусть теперь 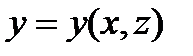найдём частную производную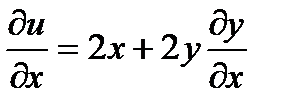

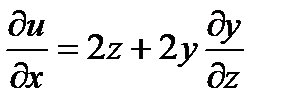, частные производные 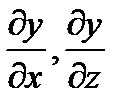найдём из условий связи.

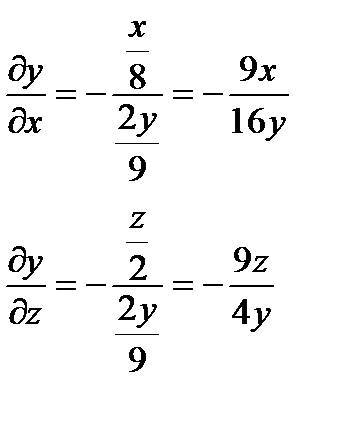
Подставляя в ранее полученные выражения, получим:

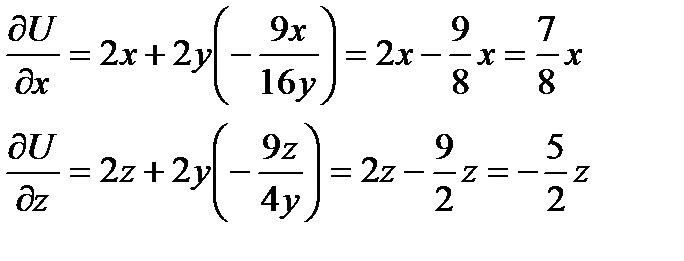
Видим, что первая производная, обращается в 0 в точках второй серии. Вычислим вторую производную в этих точках:

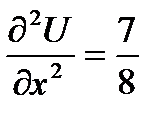
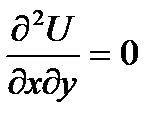
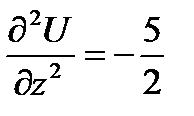
Видим, что 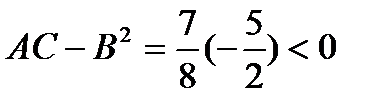- отсутствует экстремум, minimax;

Рассмотрим третий случай, вычислим производную от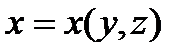

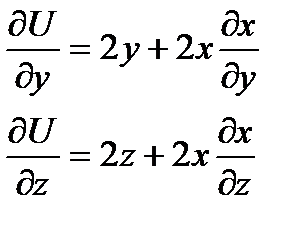
Найдём частную производную 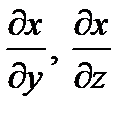по условию связей

Подставляем 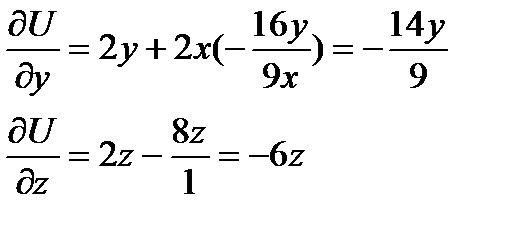обращается в 0 в точках 3-й серии. ,

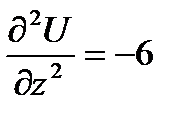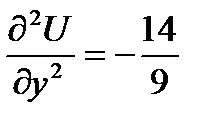
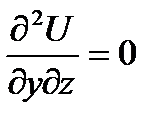
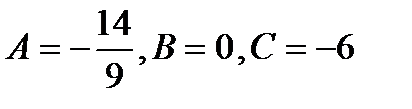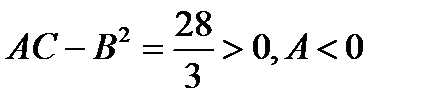, max;

Date: 2016-05-17; view: 865; Нарушение авторских прав