Исследование на экстремум функции нескольких переменных

Определение: Точка называются точкой локального максимума, если существует такая, проколотая окрестность точки M, в пределах которой выполняется неравенство:

Определение: Точка называется точкой локального минимума, если существует такая проколотая окрестность точки M, в которой:

Точки локального минимума и максимума называются точками локального экстремума.

Приведенные определения обобщаются на случай большого числа переменных.

Необходимое условие локального экстремума.

Если функция дифференцируема в некоторой окрестности т. и т. является точкой локального экстремума, то ,

Доказательство: Пусть точка является точкой локального экстремума. Рассмотрим в окрестности этой точки функцию одной переменной . Согласно определению локального экстремума для функции одной переменной. . Необходимое условие экстремума функции одной переменной. , получим условие , Аналогично доказывается, что откуда следует справедливость сделанного утверждения. Таким образом, чтобы точка была точкой локального экстремума, необходимо, чтобы первый дифференциал функции обращался в 0. Из определения точек локального экстремума, следует, что в окрестности этих точек полное приращение сохраняет свой знак.

В точке локального минимума 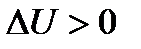. Из (7) следует, что вывод о существовании критической точки экстремума определяется с помощью рассмотрения второго дифференциала или дифференциала более высокого порядка. Пусть точка M является критической точкой функции U. (первый дифференциал в точке M=0) Полное приращение функции U точки M на основании (7) может быть представлена в виде:

Т.к. в критической точке, то вывод о наличии экстремума производится из второго дифференциала. Если точка M является точкой экстремума, то приращение функции в окрестности этой точки сохраняет знак. Отбросим бесконечно малые более высокого порядка малости .

В этом случае вопрос о наличие в точке M локального экстремума определятся значением второго дифференциала в окрестности точки M. Если второй дифференциал , то приращение в точке M и точка M будет точкой локального минимума. Если и , то M - точка локального максимума.

Рассмотрим задачу локального экстремума на конкретном примере:

Пример: 8.197

1)Находим стационарные(критические) точки функции.

В силу, сделанного ограничения:

Решаем методом Гаусса

~ ~

-критическая точка. Найдем второй дифференциал в точке M.

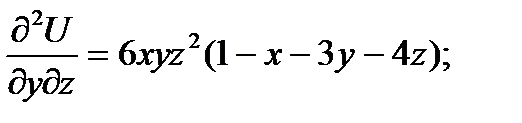
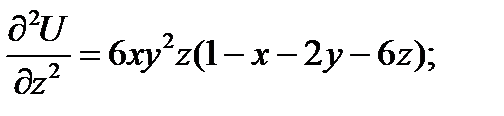
Введем следующие обозначения для двух частных производных в точке M.

Таким образом, второй дифференциал в точке M можно записать в виде:

Из курса линейной алгебры следует, что выражение в правой части называется квадратичной формой 3-х переменных.

Каждая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду. Если 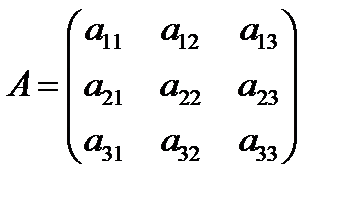матрица квадратичной формы, то в некотором ортонормированном базисе матрицу А можно записать в виде , где , , - собственные значения матрицы А.

В случае нашего примера второй дифференциал в точке М можно представить в виде:

Для нахождения собственных значений составим характеристический многочлен:

Видим, что выписанный многочлен не может иметь положительных собственных значений, все собственные значения отрицательны, таким образом, в некотором новом базисе: , где - отрицательны, следовательно второй дифференциал в точке отрицателен. Это означает, что приращение , то есть точка M является точкой локального максимума. Для установления локального максимума или минимума вычислять собственные значения необязательно. Можно воспользоваться критерием Сильвестра.

Матрица A является матрицей квадратной формы от n – переменных. Для того чтобы квадратная форма была знакоположительна, необходимо и достаточно, чтобы все её главные миноры были положительны:

С помощью критерия Сильвестра, можно определить отрицательную квадратную форму. Если отрицательно определенную квадратичную форму умножить на -1, то она превращается в положительно определённую квадратичную форму. Приведённый критерий Сильвестра для A: . Рассмотрим вспомогательную матрицу:

. Тогда для A, получим набор миноров. . Согласно критерию Сильвестра - положительная квадратичная форма, A – знакоотрицательна, и в точке M – локальный максимум. Наиболее просто вопрос существования локального экстремума решается для функции двух переменных

Date: 2016-05-17; view: 703; Нарушение авторских прав