
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения к практической работе. Функция , определенная на интервале , называется первообразной для функции , определенной на том же интервале
|
|
Функция  , определенная на интервале
, определенная на интервале  , называется первообразной для функции
, называется первообразной для функции  , определенной на том же интервале
, определенной на том же интервале  , если
, если 
Если  — первообразная для функции
— первообразная для функции  , то любая другая первообразная
, то любая другая первообразная 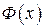 для функции
для функции  отличается от
отличается от  на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е.  где
где  .
.
Неопределенным интегралом от функции  называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 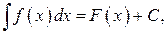 где
где 
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1. 
2. 
3. 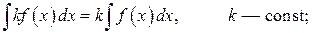
4. 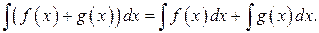
Таблица основных интегралов
1.  2.
2. 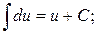
3. 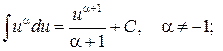
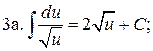
4.  5.
5. 
6.  7.
7. 
8.  9.
9. 
10.  11.
11. 
12.  13.
13. 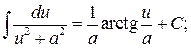
14.  15.
15. 
16.  17.
17. 
18. 
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Пример 1. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы (результат интегрирования проверить дифференцированием):


Решение.
 Проверка:
Проверка:


Проверка:
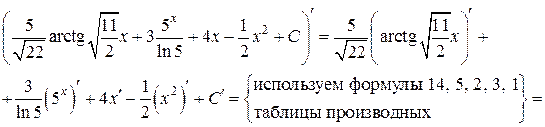

Метод замены переменной
Теорема 1. Пусть  монотонная, непрерывно дифференцируемая функция, тогда
монотонная, непрерывно дифференцируемая функция, тогда
 (1)
(1)
При этом, если  то
то  где
где  — функция, обратная
— функция, обратная  .
.
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Алгоритм замены переменной:
1) Связать старую переменную интегрирования  с новой переменной
с новой переменной  с помощью замены
с помощью замены  .
.
2) Найти связь между дифференциалами  .
.
3) Перейти под знаком интеграла к новой переменной.
4) Проинтегрировать и в полученной первообразной вернуться к старой переменной, подставив 
Пример 2. Проинтегрировать подходящей заменой переменной.



Решение:


Содержание практической работы
Задание 1. Вычислить интегралы.
1) 

2) 

3) 

4) 

5) 

6) 

Задание 2. Проинтегрировать подходящей заменой переменного.
1) 


2) 

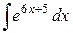
3) 

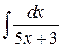
4) 


5) 


6) 


Практическая работа №11
Date: 2016-05-16; view: 630; Нарушение авторских прав