Обоснование решений по минимакс вальда

Критерий Вальда (или критерий «максимина») предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая из всех самых неблагоприятных ситуаций развития события (минимизирующих значение эффективности) имеет наибольшее из минимальных значений (т.е. значение эффективности, лучшее из всех худших или максимальное из всех минимальных).

Критерием Вальда (критерием «максимина») руководствуется при выборе рисковых решений в условиях неопределенности, как правило, субъект, не склонный к риску или рассматривающий возможные ситуации как пессимист.

2. Критерий «максимакса» предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая из всех самых благоприятных ситуаций развития событий (максимизирующих значение эффективности) имеет наибольшее из максимальных значений (т.е. значение эффективности лучшее из всех лучших или максимальное из максимальных).

Критерий «максимакса» используют при выборе рисковых решений в условиях неопределенности, как правило, субъекты, склонные к риску, или рассматривающие возможные ситуации как оптимисты.

1.1. Минимаксный критерий (ММ) использует оценочную функцию Z_ММ, соответствующую позицию крайней осторожности.

Z_ММ=max eir и eir=min eij.

где z_mm — оценочная функция ММ-критерия.

Поскольку в области технических задач построение множества Е вариантовуже само по себе требует весьма значительных усилий, причем иногда возникает необходимость в их рассмотрении с различных точек зрения. Оно должно напоминать о том, что совокупность вариантов необходимо исследовать возможно более полным образом, чтобы была обеспечена оптимальность выбираемого варианта.

Правило выбора решения в соответствии с этим критерием можно интерпретировать следующим образом:

Матрица решений дополняется еще одним столбцом из наименьших результатов e_irкаждой строки. Выбрать надлежит те варианты E_io, в строках которых стоят наибольшие значения eirэтого столбца.

Выбранные таким образом варианты полностью исключают риск. Это означает, что принимающий решение не может столкнуться с худшим результатом,чем тот, на который он ориентируется. Какие бы условияFjни встретились, соответствующий результат не может оказаться нижеZ_мм. Это свойство заставляет считать минимаксный критерий одним из фундаментальных. Поэтому в технических задачах он применяется чаще всего, как сознательно, так и неосознанно. Однако положение об отсутствии риска стоит различных потерь.

Критерий пессимизма

В случае, когда ОПР ориентируется на самые неблагоприятные условия и неконтролируемые факторы применяют критерий пессимизма.

Для игры, которую задано матрицей выигрышей по критерию пессимизма определяется вариант решения, который минимизирует минимальные выигрыши для каждого варианта ситуации. Критерий пессимизма записывают в виде

Для игры, которую задано матрицей проигрышей по критерию пессимизма определяется вариант решения, который максимизирует максимальные проигрыше для каждого варианта ситуации. Критерий пессимизма записывают в виде

По критерию пессимизма предполагается, что неконтролируемые факторы могут быть использованы неблагоприятным образом. В реальных ситуациях могут во многих задачах невозможен контроль за неконтролируемыми факторами. Это относится к задачам, в которых есть необходимость учета фактора времени; задач социально-экономического прогнозирования; задач долгосрочного планирования и тому подобное.

Например, издержки производства являются контролируемыми факторами на краткосрочных временных интервалах, но при анализе долгосрочных проектов определенные элементы издержек производства становятся неконтролируемыми: стоимость электроэнергии, стоимость материалов и т.

Пример 3.5. Для игры, которую задано матрицей выигрышей в примере 3.2, по критерию оптимизма выбрать стратегию, которая является наиболее выгодной.

Решение. Запишем матрицу выигрышей в виде таблицы 3.6 и найдем наименьшее значение minaij для каждой строки.

Таблица 3.6

Матрица выигрышей игры

По формуле (3.16) имеем:

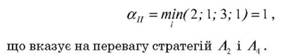
Это означает, что независимо от того какую стратегию будет применять игрок "природа", то есть который из состояний сложится на рынке, игрок А (статистик), при применении стратегий А2 и А4, то есть техники видов А2 и А4, получит гарантированный выигрыш не менее 1 единицы. При использовании игроком А любой другой стратегии, то есть выпуска другого вида техники, в случае худшего ситуации может быть получен выигрыш менее 1 единица.

Date: 2016-05-15; view: 997; Нарушение авторских прав