
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Екі белгісізі бар бірінші дәрежелі теңдеулер
|
|
Екі белгісізі бар бірінші дәрежелі теңдеуді қарастырайық:
ax + by + c = 0 (1)
Мұндағы а, b нөлден өзгеше бүтін сандар, ал с – кез – келген бүтін сан. Ал а, b коэффициенттерінің бірден басқа ортақ бөлгіші жоқ деп ұйғарайық. Шындығында, бұл коэффицентердің ең үлкен ортақ бөлгіш бірден өзгеше d = (a, b) десек, a = a1d, b = b1d теңдеулері орынды болады. Сонда (1) теңдеу мына түрге келеді: (a1x + b1y) d = 0. (2)
с саны d санына бөлінсе ғана, бұл теңдеудің бүтін шешімдері болады. Бұл жағдайда d = (a, b) ≠ 1; (2) теңдеуді d санына бөлсек, мына теңдеуді аламыз: a1x + b1y + c1 = 0 c1 =  ,
,
мұндағы a1 және b1 өзара жай сандар. Ең алдымен с = 0 болғандағы жағдайды қарастырайық. Сонда (1) теңдеу мына түрге келеді:
ax + by = 0 (1/)
Бұл теңдеуден х белгісізін табайық: х =  , х бүтін мән қабылдайды, сонда тек сонда ғана, егер у а санына қалдықсыз бөлінсе. Ал ондай у белгісізінің бүтін мәнін былай жазуға болады:
, х бүтін мән қабылдайды, сонда тек сонда ғана, егер у а санына қалдықсыз бөлінсе. Ал ондай у белгісізінің бүтін мәнін былай жазуға болады:
у = аt,
мұндағы t – кез – келген бүтін сан (t = 0,  1,
1,  2, …) у мәнін (1/) теңдеуіне қойсақ, онда
2, …) у мәнін (1/) теңдеуіне қойсақ, онда
х =  ,
,
біз (1/) теңдеуінің барлық бүтін шешімдерін қамтитын формулалар аламыз:
х = - bt, y = at (t = 0,  1,
1,  2, …)
2, …)
Енді с ≠ 0 болған жадайды қарастырамыз.
(1) теңдеудің барлық бүтін шешімдерін табу үшін, оның тек қана бір бүтін шешімін табу жеткілікті, сондай – ақ
a0x + b0y + c = 0
теңдеуі үшін х0, у0 бүтін сандарын табу керек.
Теорема 1 a және b өзара жай сандар және [ x0, y0 ] ax + by + c = 0 теңдеуінің кез – келген бүтін шешімі болсын, сонда мына формулалар:
x = x0 – bt, y = y0 + at (3)
t = 0,  1,
1,  2, … болғандағы теңдеудің барлық шешімдерін берін береді.
2, … болғандағы теңдеудің барлық шешімдерін берін береді.
Дәлелдеу: [ x, y ] - (1) теңдеудің кез – келген шешімі болсын. Сонда ax + by + c = 0 және ax0 + by0 + c = 0 теңдіктерінен мынау шығады:
ax - ax0 + by - b0 = 0, y – y0 =  ,
,
мұндағы у – у0 бүтін сан және a, b өзара жай сандар болғандықтан, х0 –х
b санына бүтіндей бөлінуі керек. Сонда х0 –х мына түрге келеді:
х – х0 = bt,
мұндағы t бүтін сан, х0 –х мәнін алдыңғы теңдікке алып барып қойсақ:
y – y0 =  .
.
сонда x = x0 – bt, y = y0 + at формулаларын аламыз.
Мысалы: 127х – 52у + 1 теңдеуі берілсін.
Бұл теңдеуді шешу үшін белгісіз мүшелердің коэффициенттерінің қатынасын алайық. Ең алдымен  бұрыс бөлшегінің бүтін бөлігін ажыратып алайық:
бұрыс бөлшегінің бүтін бөлігін ажыратып алайық:
 =
= 
Ал  дұрыс бөлшегін осы бөлшекке тең
дұрыс бөлшегін осы бөлшекке тең  бөлшегімен алмастырып, осы процесті үздіксіз жалғастырсақ, мынандай шектеулі тізбек аламыз:
бөлшегімен алмастырып, осы процесті үздіксіз жалғастырсақ, мынандай шектеулі тізбек аламыз:

Бұл бөлшек тізбегінен  бөлшегін алып тастасақ, жаңа жай бөлшек аламыз:
бөлшегін алып тастасақ, жаңа жай бөлшек аламыз:

Шыққан бөлшекті алдыңғы  бөлшегінен шегереміз:
бөлшегінен шегереміз:
 -
- 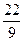 =
= 
теңдіктің екі жағын да 52∙9 санына көбейтсек,
127х – 52у + 1 = 0
теңдеуіне мәндес
127∙9 – 52∙22 + 1 = 0
теңдігін аламыз.
Бұдан х = 9, у = 22 теңдеуінің бүтін шешімі болады және теоремаға сәйкес барлық шешімдері мына прогрессияда жатады:
х = 9 + 52t, у = 22 + 127 t, t = 0,  1,
1,  2, ….
2, ….
Алынған нәтиже бізге мынадай ой туғызады:
Жалпы жағдайда ax + by + c = 0 теңдеуінің шешімдерін табу үшін, белгісіз мүшелерінің коэффициенттерінің қатынасын шектеулі тізбекке жіктеу керек, ең соңғы мүшелерін алып тастап, жоғарыда көрсетілгендей амалдар орындау керек.
Бұл пайымдауды дәлелдеу үшін шектеулі тізбектің кейбір қасиеттері қажет болады.
Қысқармайтын  бөлшегін қарастырайық, ондағы а санын b санына бөлгендегі бөліндіні q1 деп, қалдық мүшесін r2 деп белгілейік, сонда
бөлшегін қарастырайық, ондағы а санын b санына бөлгендегі бөліндіні q1 деп, қалдық мүшесін r2 деп белгілейік, сонда
а = q1 b + r2, r2 < b.
Енді, ары қарай, b санын r2 қалдығына бөлгендегі бөліндіні q2 деп, аламыз, сонда
b = q2 r2 + r3, r3 < r2.
Дәл осылай жалғастырсақ:
r2 = q3 r 3 + r4 , r4 < r3
r3 = q4 r 4 + r5, r5 < r4
.........................................
Бұл процесс Евклид алгоритмі деп аталады, q1, q2,... өлшемдері толық емес бөлінділер және r2, r3 қалдықтары мына теңсіздіктерді қанағаттандырады:
b > r2 > r3 > r4 > … > 0 (4)
Осылай теріс емес кемімелі сандар қатары құрылады, ал rn (4) қатардағы ең соңғы нөлден өзге қалдық болсын, сонда rn+1 = 0 және a, b сандары үшін Евклид алгоритмі мына түрге келеді:
 а = q1 b + r2
а = q1 b + r2
b = q2 r2 + r3
r2 = q3 r 3 + r4 (5)
........................
rn-2 = q n-1 r n-1 + r n
rn-1 = q n r n.
Алынған теңдіктерді мына түрде жазайық:

Бірінші қатардағы  бөлшегін соған тең екінші қатардағы мәнімен алмастырсақ, ал
бөлшегін соған тең екінші қатардағы мәнімен алмастырсақ, ал  бөлшегін үшінші қатардағы мәнімен алмастырсақ және тағы сол сияқты жалғастырсақ, онда
бөлшегін үшінші қатардағы мәнімен алмастырсақ және тағы сол сияқты жалғастырсақ, онда  бөлшегінің келесі бөлшек тізбегіне жіктелуін аламыз:
бөлшегінің келесі бөлшек тізбегіне жіктелуін аламыз:

Алынған бөлшек тізбегінің кейбір мүшелерінен бастап барлық мүшелерін алып тастағанда қалатын өрнекті лайықты бөлшек деп атаймыз. Бірінші лайықты бөлшек  бөлшегінен бастап барлық мүшелерін алып тастағанда шығады:
бөлшегінен бастап барлық мүшелерін алып тастағанда шығады:
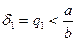
Екінші лайықты бөлшек  бөлшегінен бастап барлық мүшелерін алып тастағанда шығады:
бөлшегінен бастап барлық мүшелерін алып тастағанда шығады:

Дәл осылай
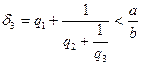

және т.с.с. жалғаса береді. Лайықты бөлшектердің құрылуына байланысты келесі теңсіздіктер орын алады:
 <
<  < … <
< … < 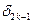 <
<  ,
,  >
>  > … >
> … >  >
> 
Лайықты 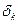 бөлшегін мына түрде жазсақ:
бөлшегін мына түрде жазсақ:
 (1 ≤ к ≤ n),
(1 ≤ к ≤ n),
лайықты бөлшектің алымы мен бөлімінің құрылу заңдылығын табамыз. Енді  ,
,  және
және  бөлшектерін түрлендірейік:
бөлшектерін түрлендірейік:
 =
=  ; P1 = q1, Q1 = 1;
; P1 = q1, Q1 = 1;
 =
=  ;
;
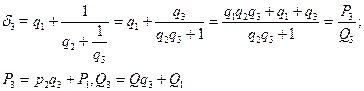
Индукция әдісін қолдансақ, барлық к≥3 үшін мына қатыстың орынды екенін дәлелдейміз:
P k = Pk-1 q k + P k-1 , Q k = Qk-1 q k + Q k-2 (6)
Шындығында, (6) теңдік кейбір к≥3 үшін ғана орынды болсын. Лайықты бөлшектердің анықтамасы бойынша, 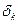 өрнегіндегі q k өлшемін
өрнегіндегі q k өлшемін  өлшемімен алмастырсақ,
өлшемімен алмастырсақ, 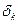 лайықты бөлшегі
лайықты бөлшегі  лайықты бөлшегіне ауысады. Индукция әдісін қолданайық:
лайықты бөлшегіне ауысады. Индукция әдісін қолданайық:
 .
.
 =
=  екені белгілі болғандықтан,
екені белгілі болғандықтан,
Pk+1= P k q k+1 + Pk-1, Q k+1= Q k q k+1 + Q k-1
Осы әдіспен (6) теңдіктің к+1 үшін орынды екенін көрдік.Сол сияқты барлық к≥3 үшін де орынды.
Енді көршілес 2 лайықты бөлшектің айырымы мына қатынасты қанағаттандыратынын көрсетейік:
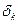 -
-  =
= 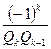 (к>1) (7)
(к>1) (7)
Шындығында,
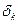 -
-  =
=  -
-  =
= 
(6) формуланы пайдаланып, бөлшектің алымын түрлендіреміз:
 =
=  .
.
Алынған өрнектерге осындай түрлендірулерді қайта жүргізсек, келесі теңдіктер тізбегін аламыз:
 =
=  =
=  =... =
=... =  =
= 
Осыдан келіп
 -
-  =
=  =
= 
екендігі шығады.
Егер  бөлшегін бөлшек тізбегіне жіктегенде n мүшесі болса, онда n –ші лайықты бөлшек
бөлшегін бөлшек тізбегіне жіктегенде n мүшесі болса, онда n –ші лайықты бөлшек 
 бөлшегімен сәйкес келеді. (7) теңдікті қолданып, к = n деп жазамыз:
бөлшегімен сәйкес келеді. (7) теңдікті қолданып, к = n деп жазамыз:

 -
-  =
=  (8)
(8)
 -
- 


Енді ax + by + c = 0 теңдеуінің шешіміне келеміз, мұндағы (a, b) = 1. (8) қатынасты мына түрде жазамыз:
 -
-  =
= 
Теңдіктің 2 жағын да  өрнегіне көбейтеміз:
өрнегіне көбейтеміз:
aQn-1 – bPn-1 = (-1)n
aQn-1 + b(-Pn-1) + (-1)n = 0
Шыққан теңдікті (-1)n-1 с с – санына көбейтеміз:
a [ (-1)n-1 Qn-1 ] + b [ (-1)n c Pn-1 ] + c = 0
осыдан келіп
x0 = (-1)n c Qn-1, y0 = (-1)n c Pn-1 (9)
(1) теңдеудің шешімдері болады және теоремаға
сәйкес барлық шешімдері мына түрде жазылады:
x = (-1)n c Qn-1 - bt, y = (-1)n c Pn-1 + at,
мұндағы t = 0,  1,
1,  2, ….
2, ….
Шыққан нәтиже барлық 2 белгісізі бар бірінші дәрежелі теңдеулердің барлық бүтін шешімдерін табу туралы сұрақтың жауабын береді.
І нұсқа ІІ нұсқа
1.Теңдеуді шешіңдер  1.Теңдеуді шешіңдер
1.Теңдеуді шешіңдер 
2.Тепе – теңдікті дәлелдеңдер


3. Теңсіздікті шешіңдер:
(x+7)(x+4)2(x-2)<0 (x-3)(x-4)2(x-10)<0
Бөлшекті қысқартыңдар:

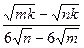
І нұсқа ІІ нұсқа
1. Есептеңдер:
а)  а)
а) 
ә)  ә)
ә) 
б)  б)
б) 
2. Салыстырыңдар:
а)  және
және 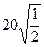 а)
а)  және
және 
ә)  және
және 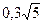 ә)
ә)  және
және 
3. Теңдеудің рационал түбірлерін табыңдар:
х4 – 7х2 + 12 = 0 х4 – 16х2 + 63 = 0
Бөлшекті қысқартыңдар:
18х2-3х-21 28х2-27х+5
18х2-33х+14 28х2-48х+20
09.09.15
Date: 2016-06-09; view: 2461; Нарушение авторских прав