Функцияның қасиеттері

1. Егер берілген облыста әрбір х үшін f(-x) = f(x) теңдігі орындалса, онда f(х) функциясын осы облыста жұп функция деп, ал f(-х)= - f(х) болса, онда тақ функция деп атайды.

Мысалы, у = х² функциясы барлық сан осінде жұп функция болады, өйткені f(-х)=(-х)² =х² =f(х), ал у = х³ функциясы тақ функция, өйткені f(-х) = (-х)³ = -х³ = -f(х).

Ал у = х² - х³ функциясы жұп та, тақ та емес, өйткені f(-x) = (-х)² - (-х)³ = х² + х³ ≠ f(х).

Жұп функцияның графигі ордината осіне қарағанда, ал тақ функцияның графигі бас нүктеге қарағанда симметриялы болады.

Мысалы, у = |х| функциясы жұп функция, өйткені у(-х) = |- х| = |х| = у(х). Оның графигі ордината осіне карағанда симметриялы (6.6-сурет).

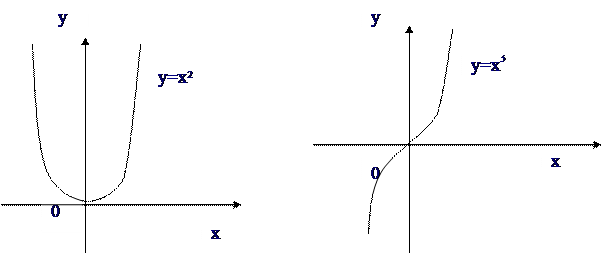6.6 сурет

2. Егер берілген облыста кез келген х үшін f(х + Т) = f(x) теңдігі орындалса, онда f(х) функциясы осы облыста периодты функция деп аталады.

Мұндағы Т≠О— нақты сан, ол функцияның периоды деп аталады.

Мысалы, y = sin2х функциясы периодты, оның периоды Т = π болады, өйткені sin2(х +π ) = sin(2х + 2π) = sin 2х.

3. Егер X жиынында жатқан кез келген х₁ мен х₂ мәндері үшін х₁ < х₂ теңсіздігінен f(х₁)<f(х₂) f(x₁) ≤f(х₂)) теңсіздігі шықса, онда f(х) функциясын X жиынында өспелі (кемімейтін), ал егер X жиынында жатқан кез келген х₁ мен х₂ мәндері үшін х₁<х₂ теңсіздігіненегер f(x₁)>f(x₂) (f(x₁) ≥ f(x₂)) теңсіздігі шықса, онда кемімелі (өспейтін) функция дейді.

ƒ(x₁)> ƒ(x₂), (ƒ(x₁)≥ƒ(x₂)).

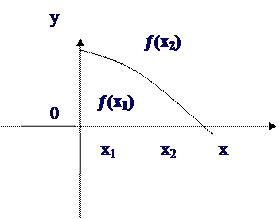Осы функциялар монотонды функциялар деп аталады.

Мысалы, у = х² функциясы аралығында кемімелі, ал [0, ∞) аралығында өспелі функция.

Егер X аралығында жаткан барлық х нүктелері үшін |f(x)|≤M теңсіздігі орындалатындай М>0 саны табылса, онда f(x) функциясы X аралығында шенелген функция деп аталады. Мысалы, у = соs3х функциясы барлық нақты сандар жиыны R – де шенелген, өйткені кез келген х 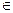R үшін

|соs3x| ≤ 1.

Айқын емес функция

Егер ƒ(x;у) =0, теңдеуі у функциясы бойынша шешіліп тұрмаса, онда х аргументінің айқын емес функциясы деп аталады

Sinx + ху=4

30.09